LearningActivities ColorBlindness
From Socr
Contents |
Distributome Learning Activities - Distributome Colorblindness Activity
Overview
This Distributome Activity illustrates an application of probability theory to study Colorblindness.
Colorblindness results from an abnormality on the X chromosome. The condition is thus rarer in women since a woman would need to have the abnormality on both of her X chromosomes in order to be colorblind (whether a woman has the abnormality on one X chromosome is essentially independent of having it on the other).
Goals
The goal of this activity is to demonstrate an efficient protocol of estimating the probability that a randomly chosen individual may be colorblind.
Hands-on Activity
Suppose that p is the probability that a randomly selected man is colorblind.
- 100 men are selected at random. What is the distribution of Xm = the number of these men that are colorblind?
- Xm~Binomial(100,p).
- 100 women are selected at random. What is the distribution of Xf = the number of these women that are colorblind?
- Hint: the chance that an individual woman is colorblind is p2, why?
- Solution: Xf~Binomial(100,p2)
- To estimate the probability that a randomly selected woman is colorblind, you might use the proportion of colorblind women in a sample of n women. What is the variance of this estimator?
- Xf~Binomial(n,p2). Thus
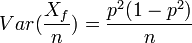 .
.
- Xf~Binomial(n,p2). Thus
- Alternatively, to estimate the probability that a randomly selected woman is colorblind, you might use the square of the proportion of colorblind men in a sample of n men. Explain why this estimate makes sense. What is the variance of this estimator?
- Hint: The moment generating function can be used to find the fourth moment about the origin.
- Hint: We want to estimate p2 and
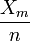 estimates p so it makes sense to use Failed to parse (lexing error): \left \(\frac{X_m}{n}\right\)^2
estimates p so it makes sense to use Failed to parse (lexing error): \left \(\frac{X_m}{n}\right\)^2
as the estimator (in fact it will be the maximum likelihood estimate). We have Var[( XM n )2 ] = n!4[E(XM 4 ) ! (E(XM 2 ))2 ].Take q=1--?p. Then the fourth moment about the origin of a binomial is E(X4)= np(q--?6pq2+7npq--?11np2q+6n2p2q+n3p3) and the second moment is E(X2)=np(q+np). Thus Var[( XM n )2 ] = n!3(pq + 6(n !1)p2q2 + 4n(n !1)p3q).
- For large samples, is it better to use a sample of men or a sample of women to estimate the probability that a randomly selected women is colorblind? Explain.
Hint: Show that a normal approximation is valid for both and then compare the variances.
Solution: For large n the ratio of the variances for the estimate in part c to the estimate in part d is Var(XF / n) Var((XM / n)2 ) ! p2 (1" p2 ) 4p3q = 1+ p 4p . When this ratio is greater than 1, the estimator based on the sample of men will be better. Since this happens for any p< 1/3, which is clearly the case for colorblindness, it is better to use a sample of men to estimate the probability that a random woman is colorblind.
Conclusions
You can also use the delta method to find the approximate variance for the estimator above.
Translate this page:
