SOCR Courses 2011 2012 Stat13 1 Lab6
From Socr
Contents |
Stats 13.1 - Laboratory Activity 6
Central Limit Theorem (CLT) Activity
This activity represents a very general demonstration of the the Central Limit Theorem (CLT). The activity is based on the SOCR Sampling Distribution CLT Experiment. This experiment builds upon a RVLS CLT applet by extending the applet functionality and providing the capability of sampling from any SOCR Distribution.
Goals
The aims of this activity are to:
- Provide intuitive notion of sampling from any process with a well-defined distribution.
- Motivate and facilitate learning of the central limit theorem.
- Empirically validate that sample-averages of random observations (most processes) follow approximately normal distribution.
- Empirically demonstrate that the sample-average is special and other sample statistics (e.g., median, variance, range, etc.) generally do not have distributions that are normal.
- Illustrate that the expectation of the sample-average equals the population mean (and the sample-average is typically a good measure of centrality for a population/process).
- Show that the variation of the sampling distribution of the mean rapidly decreases as the sample size increases (
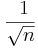 ).
).
- Reinforce the concepts of a native distribution, sample, sample distribution, sampling distribution, parameter estimator and data-driven numerical parameter estimate.
The SOCR CLT Experiment
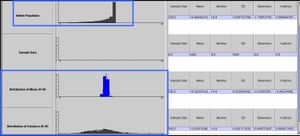
To start the this Experiment, go to SOCR Experiments and select the SOCR Sampling Distribution CLT Experiment from the drop-down list of experiments in the left panel. The image below shows the interface to this experiment. Notice the main control widgets on this image (boxed in blue and pointed to by arrows). The generic control buttons on the top allow you to do one or multiple steps/runs, stop and reset this experiment. The two tabs in the main frame provide graphical access to the results of the experiment (Histograms and Summaries) or the Distribution selection panel (Distributions). Remember that choosing sample-sizes <= 16 will animate the samples (second graphing row), whereas larger sample-sizes (N>20) will only show the updates of the sampling distributions (bottom two graphing rows).
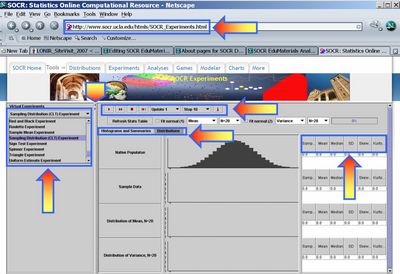
Experiment 1
Expand your Experiment panel (right panel) by clicking/dragging the vertical split-pane bar. Choose the two sample sizes for the two statistics to be 10. Press the step-button a few of times (2-5) to see the experiment run several times. Notice how data is being sampled from the native population (the distribution of the process on the top). For each step, the process of sampling 2 samples of 10 observations will generate 2 sample statistics of the 2 parameters of interest (these are defaulted to mean and variance). At each step, you can see the plots of all sample values, as well as the computed sample statistics for each parameter. The sample values are shown on the second row graph, below the distribution of the process, and the two sample statistics are plotted on the bottom two rows. If we run this experiment many times, the bottom two graphs/histograms become good approximations to the corresponding sampling distributions. If we did this infinitely many times these two graphs become the sampling distributions of the chosen sample statistics (as the observations/measurements are independent within each sample and between samples). Finally, press the Refresh Stats Table button on the top to see the sample summary statistics for the native population distribution (row 1), last sample (row 2) and the two sampling distributions, in this case mean and variance (rows 3 and 4).
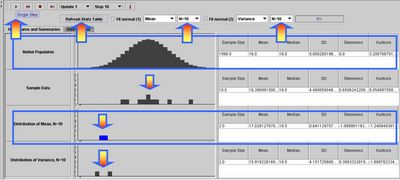
Experiment 2
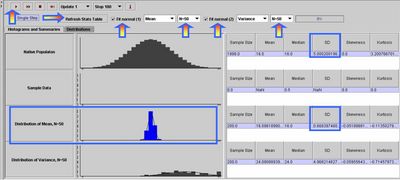
For this experiment we'll look at the mean, standard deviation, skewness and kurtosis of the sample-average and the sample-variance (these two sample data-driven statistical estimates). Choose sample-sizes of 50, for both estimates (mean and variance). Select the Fit Normal Curve check-boxes for both sample distributions. Run through the experiment 10 times (by clicking the Run button and selecting Stop 10) and then click Refresh Stats Table button on the top to see the sample summary statistics. Run again 100 times by selecting Stop 100 instead of Stop 10. Try to understand and relate these sample-distribution statistics to their analogues from the native population (on the top row). For example, the mean of the multiple sample-averages is about the same as the mean of the native population, but the standard deviation of the sampling distribution of the average is about 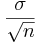 , where σ is the standard deviation of the original native process/distribution.
, where σ is the standard deviation of the original native process/distribution.
Question 1: Verify that the standard deviation of the sampling distribution of the average is about 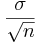 after running the experiment 100 times, where σ is the standard deviation of the original native process/distribution.
after running the experiment 100 times, where σ is the standard deviation of the original native process/distribution.
Experiment 3
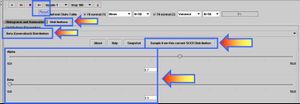
Now let's select any of the SOCR Distributions, sample from it repeatedly and see if the central limit theorem is valid for the process we have selected. Try Poisson, Beta, Gamma, Cauchy and other continuous or discrete distributions. Choose a sample size 50 or bigger. Are our empirical results in agreement with the CLT? Go to the Distributions tab on the top of the graphing panel. Reset the experiments panel (button on the top). Select a distribution from the drop-down list of distributions in this list. Choose appropriate parameters for your distribution, if any, and click the Sample from this Current Distribution button to send this distribution to the graphing panel in the Histograms and Summaries tab. Go to this panel and again run the experiment several times. Notice how we now sample from a Non-Normal Distribution for the first time. In this case we had chosen the Beta distribution (α = 6.7,β = 0.5).
Question 2: Take a snapshot of the experiment using one of the distributions mentioned above. Verify that the standard deviation of the sampling distribution of the average is about 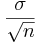 , where σ is the standard deviation of the original native process/distribution.
, where σ is the standard deviation of the original native process/distribution.
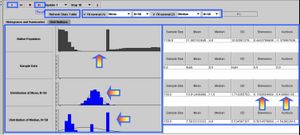
Experiment 4
Suppose the distribution we want to sample from is not included in the list of SOCR Distributions, under the Distributions tab. We can then draw a shape for a hypothetical distribution by clicking and dragging the mouse in the top graphing canvas (Histograms and Summaries tab panel). Choose a sample size 50 or bigger. This way you can construct continuous and discontinuous, symmetric and asymmetric, unimodal and multi-modal, leptokurtic and mesokurtic and other types of distributions. In the figure below, we had demonstrated this functionality to study differences between two data-driven estimates for the population center - sample mean and sample median. Look how the sampling distribution of the sample-average is very close to Normal, where as the sampling distribution of the sample median is not.
Question 3: Take a snapshot of an experiment where you create your own distribution. Verify that the standard deviation of the sampling distribution of the average is about 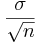 , where σ is the standard deviation of the original native process/distribution.
, where σ is the standard deviation of the original native process/distribution.
Questions
- What effects will asymmetry, gaps and continuity of the native distribution have on the applicability of the CLT, or on the asymptotic distribution of various sample statistics?
Answering the following questions is optional:
- When can we reasonably expect statistics, other than the sample mean, to have CLT properties?
- If a native process has σX = 10 and we take a sample of size 10, what will be
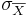 ? Does it depend on the shape of the original process? How large should the sample-size be so that
? Does it depend on the shape of the original process? How large should the sample-size be so that 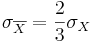 ?
?
Applications
The second part of this SOCR Activity demonstrates the applications of the Central Limit Theorem.
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
