SOCR EduMaterials Activities ChuckALuckExperiment
From Socr
Contents |
Chuck A Luck Experiment
Description
The game of Chuck-A-Luck begins when a gambler chooses an integer from the interval 1 to 6. Three fair dice are then rolled. If exactly k dice show the gambler’s number, the payoff is k:1.
In the first picture box, the three dice are shown on each update. Random variable W gives the gambler’s net profit on a $1 bet and it is recorded in the first table after each run.
In the second picture box, the density and moments of W are shown in blue, and are recorded in the second table. Also, the empirical density of W is shown in red in the second picture box and it is recorded in the second table.
Goal
The purpose of this experiment is to provide a useful simulation similar to the unequal game of chance, Chuck-A-Luck. After running the experiment many times, the user should realize that even if the dice are fair, the players are more likely to lose more than they win.
Experiments
Go to the SOCR Experiment and select the Chuck A Luck Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
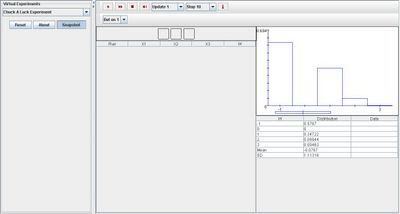
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
Selecting an integer as the player’s bet does not change the shapes of the graphs. After many trials, the empirical density of W will always be approximate to the graphs of density and moments of W. The image below displays this statement:
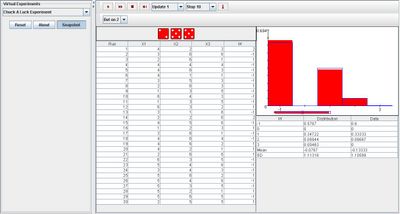
The player should take note that whichever integer has been chosen, the mean value of data is most always negative, proving that the chances for the player to win is very unlikely.
Applications
The Chuck A Luck Experiment provides a simply java applet that allows the user to play an unequal game of chance. It could be used to verify the player’s winning expectations, but in the end, the casino has a much greater advantage than the player. The experiment could also be used for the game of Big Six Wheel as it is based on the game of Chuck-A-Luck.
Probability calculations
Let's now discuss the probability model for the Chuck A Luck Experiment. How can we compute the expectation of this game? Is the player expected to win or loose money (on the long run)?
Let's first look at the outcomes of each experiment and compute the corresponding outcome probability values. Then, we can use the expectation formula to compute the expected return (expected value) for this experiment. A zero, positive or negative expected return indicates if the game is fair, or biased for the player or the house, respectively.
The table below identifies the possible outcomes of this experiment and shows how to use the Binomial Distribution to compute their corresponding probabilities. Note that the probability of a single die turning up and matching (or not matching, the complementary event) the player betting number is \(\frac{1}{6}\) (or \(\frac{5}{6}\)).
| Outcome = Number of matching dice | None=loss | 1 | 2 | 3 |
| X (profit/payoff) | -1 | 1 | 2 | 3 |
| P(X=x) | \( \left( \frac{5}{6} \right)^3 \) | \(\binom{3}{1} \left( \frac{5}{6} \right)^2 \frac{1}{6}\) | \(\binom{3}{2}\frac{5}{6} \left( \frac{1}{6} \right)^2 \) | \( \left(\frac{1}{6}\right)^3 \) |
| x*P(X=x) | (-1)x0.5787 | 0.34722 | 2x0.06944 | 3x0.00463 |
Thus, if X is the random variable denoting the return of this game (player's profit), its expected value is:
- \( E[X]=\sum_x{xP(X=x)} = -0.0787\).
Similarly, we can compute the variance and standard deviation of the outcome/payoff variable X:
- \( Var[X]= 1.23917\) and \( SD[X]= 1.11318 = \sqrt{Var[X]}\).
What is your interpretation of this quantitative analysis of the Chuck A Luck Experiment? Would you agree to play (or host) this game?
Translate this page:
