SOCR EduMaterials Activities SignTestExperiment
From Socr
Contents |
Sign Test Experiment
Description
The experiment is to select a random sample of size n from a distribution, and then to perform a hypothesis test about the median m of the distribution at a specified significance level. The distribution can be selected from a list box; the options are the N(μ,σ2), Γ, and uniform distributions. In each case, the appropriate parameters and the sample size n can be varied with scroll bars. The significance level can be selected with a list box. The null hypothesized value m0 of the median can be selected with a scroll bar; the true quantile level p of m0 is also given. The density of the distribution and m are shown in blue in the first graph; m0 is shown in green. The test statistic N is the number of sample values greater than m0. Under the null hypothesis, N has the binomial distribution with parameters n and 1/2. The density of this distribution and the critical values are shown in the second graph in blue. On each update, the sample density is shown in red in the first graph and the sample values are recorded in the first table. The value of the test statistics N is shown in red in the second graph. The variable J indicates the event that the null hypothesis is rejected. On each update, N and J are recorded in the second table. Note that the null hypothesis is reject (J = 1) if and only if the test statistic N falls outside of the critical values. Finally, the empirical density of I is shown in red in the last graph and recorded in the last table.
Goal
The Sign Test Experiment provides a simulation regarding hypothesis testing under different forms of distribution. It facilitates others to learn and understand statistics more, and in result develop a generalization of hypothesis testing.
Experiment
Go to the SOCR Experiment [SOCR Experiment] and select the Sign Test Experiment from the drop-down list of experiments on the top left. The image below shows the initial view of this experiment:
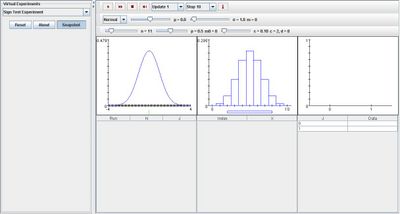
When pressing the play button, one trial will be executed and recorded in the distribution table below. The fast forward button symbolizes the nth number of trials to be executed each time. The stop button ceases any activity and is helpful when the experimenter chooses “continuous,” indicating an infinite number of events. The fourth button will reset the entire experiment, deleting all previous information and data collected. The “update” scroll indicates nth number of trials (1, 10, 100, or 1000) performed when selecting the fast forward button and the “stop” scroll indicates the maximum number of trials in the experiment.
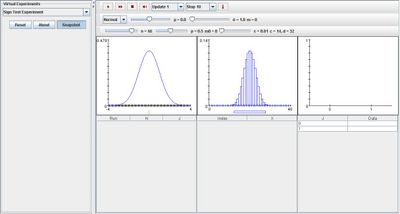
For the distribution graphs, only changes in parameter n affects the shapes of the graphs. When parameter n is increased, the graph on the right carries more values thus it will take on forms that are more curved and more normal. The image below illustrates this:
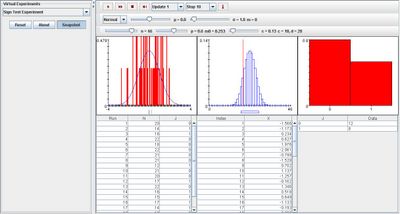
When modifying parameter p, it affects the third image in such a way that when p takes on values at its extremities, the proportion of 1 is very large while 0 has little or no value. With p at its median, the proportion of 0 and 1 are almost equal with the exception that 0 has a higher value than 1. The image below demonstrates this:
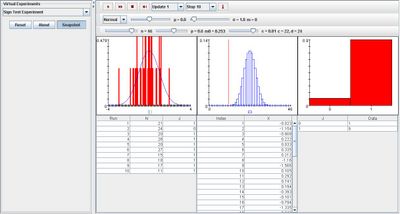
But with alpha obtaining a large value, the proportion of 1 increases and the proportion of 0 severely decreases where it has little or no value. The image below demonstrates this:
These properties are applicable for all the three distributions with little adjustments or approximations. Overall, they demonstrate the same characteristics of the Sign Test Experiment as well as hypothesis testing.
Applications
The Sign Test Experiment is a simulation that may be used in many different types of situations consisting of hypothesis testing and normal, gamma, or uniform distributions such as:
A student wants to test his hypothesis in an experiment regarding the number of times he will randomly select a red sock from his sock drawer. He theorizes that it will take him at most three tries but by using this simulation a few times, he can easily determine the amount of times required to randomly select a red sock.
A customer wants to test his hypothesis of consumers selecting the cheapest can of soda in a super market. Using this simulation can help present his findings in a more formal approach.
Translate this page:
