AP Statistics Curriculum 2007 ANOVA 1Way
From Socr
(→Motivational Example) |
|||
| Line 42: | Line 42: | ||
Using ANOVA, the data are regarded as random samples from ''k'' populations. Suppose the population means of the samples are <math>\mu_1, \mu_2, \mu_3, \mu_4, \mu_5</math> and their population standard deviations are: <math>\sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5</math>. We have 5 group means to compare. Why not just carry out <math>{5\choose 2}=10</math> T-tests comparing all (independent) pairs of groups? | Using ANOVA, the data are regarded as random samples from ''k'' populations. Suppose the population means of the samples are <math>\mu_1, \mu_2, \mu_3, \mu_4, \mu_5</math> and their population standard deviations are: <math>\sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5</math>. We have 5 group means to compare. Why not just carry out <math>{5\choose 2}=10</math> T-tests comparing all (independent) pairs of groups? | ||
| - | Repeated T-tests would mean testing | + | Repeated T-tests would mean testing null hypotheses of the type <math>H_o: \mu_i = \mu_j, \forall i\not= j</math>. What is the problem with this approach? Suppose each test is carried out at <math>\alpha = 0.05</math>, so a [[AP_Statistics_Curriculum_2007_Hypothesis_Basics | type I error]] is 5% for each test. |
Then, the overall risk of a type I error is larger than 0.05 and gets much larger as the number of groups (''k'') gets larger. To solve this problem, we need to make multiple comparisons with an overall error of <math>\alpha = 0.05</math> (or whichever level is specified initially). | Then, the overall risk of a type I error is larger than 0.05 and gets much larger as the number of groups (''k'') gets larger. To solve this problem, we need to make multiple comparisons with an overall error of <math>\alpha = 0.05</math> (or whichever level is specified initially). | ||
| Line 53: | Line 53: | ||
It is very important that we keep these two types of variability in mind as we work through the following formulas. It is our goal to come up with a numerical recipe that describes/computes each of these variabilities. | It is very important that we keep these two types of variability in mind as we work through the following formulas. It is our goal to come up with a numerical recipe that describes/computes each of these variabilities. | ||
| - | |||
===One-Way ANOVA Calculations=== | ===One-Way ANOVA Calculations=== | ||
Revision as of 20:51, 28 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - One-Way Analysis of Variance (ANOVA)
In the two-sample inference chapter, we considered the comparisons of two independent group means using the Independent T-test. Now, we expand our inference methods to study and compare k independent samples. In this case, we will be decomposing the entire variation in the data into (independent/orthogonal) components - i.e., we'll be analyzing the variance of the data. Hence, this procedure called Analysis of Variance (ANOVA).
Motivational Example
Suppose 5 varieties of peas are currently being tested by a large agribusiness cooperative to determine which is best suited for production. A field was divided into 20 plots, with each variety of peas planted in four plots. The yields (in bushels of peas) produced from each plot are shown in two identical forms in the tables below.
| Variety of Pea | ||||
| A | B | C | D | E |
| 26.2 | 29.2 | 29.1 | 21.3 | 20.1 |
| 24.3 | 28.1 | 30.8 | 22.4 | 19.3 |
| 21.8 | 27.3 | 33.9 | 24.3 | 19.9 |
| 28.1 | 31.2 | 32.8 | 21.8 | 22.1 |
| A | 26.2,24.3,21.8,28.1 |
| B | 29.2,28.1,27.3,31.2 |
| C | 29.1,30.8,33.9,32.8 |
| D | 21.3,22.4,24.3,21.8 |
| E | 20.1,19.3,19.9,22.1 |
Using the SOCR Charts (see SOCR Box-and-Whisker Plot Activity and Dot Plot Activity), we can generate plots that enable us to compare visually the yields of the 5 different types peas.
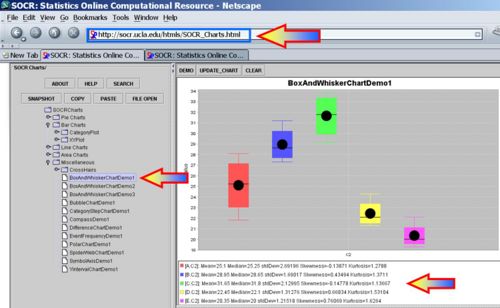
Using ANOVA, the data are regarded as random samples from k populations. Suppose the population means of the samples are μ1,μ2,μ3,μ4,μ5 and their population standard deviations are: σ1,σ2,σ3,σ4,σ5. We have 5 group means to compare. Why not just carry out 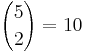 T-tests comparing all (independent) pairs of groups?
T-tests comparing all (independent) pairs of groups?
Repeated T-tests would mean testing null hypotheses of the type 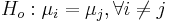 . What is the problem with this approach? Suppose each test is carried out at α = 0.05, so a type I error is 5% for each test.
Then, the overall risk of a type I error is larger than 0.05 and gets much larger as the number of groups (k) gets larger. To solve this problem, we need to make multiple comparisons with an overall error of α = 0.05 (or whichever level is specified initially).
. What is the problem with this approach? Suppose each test is carried out at α = 0.05, so a type I error is 5% for each test.
Then, the overall risk of a type I error is larger than 0.05 and gets much larger as the number of groups (k) gets larger. To solve this problem, we need to make multiple comparisons with an overall error of α = 0.05 (or whichever level is specified initially).
The main idea behind ANOVA is that we need to know how much inherent variability exists is in the data before we can judge whether there is a difference in the sample means - i.e., presence of a grouping effect. To make an inference about means we compare two types of variability:
- Variability between sample means
- Variability within each group
It is very important that we keep these two types of variability in mind as we work through the following formulas. It is our goal to come up with a numerical recipe that describes/computes each of these variabilities.
One-Way ANOVA Calculations
Let's make the following notation:
- yi,j = the measurement from group i, observation-index j.
- k = number of groups
- ni = number of observations in group i
- n = total number of observations,
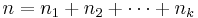
- The group mean for group i is:
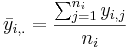
- The grand mean is:
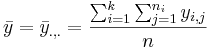
To compute the difference between the means, we will compare each group mean to the grand mean.
- SST (Sum Square due to Treatment, or Between Group variation):
First, we describe the variation between the group means. For the independent T-test we described the difference between two group means as 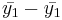 . In ANOVA we describe the difference between k means as sums of squares due to treatments (or between-group variance):
. In ANOVA we describe the difference between k means as sums of squares due to treatments (or between-group variance):
- SST(Between) =
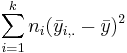 . SST can be thought of as the difference between each group mean and the grand mean.
. SST can be thought of as the difference between each group mean and the grand mean.
- Degrees of Freedom: df (Between) = k – 1.
- Mean Sum Square due to Treatment (Between):
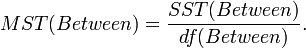 This measures variability between the sample means.
This measures variability between the sample means.
- SSE (Sum Square due to Error, or Within Group Variation):
Second, we assess the within group variation. Recall that to measure the variability within a single sample we used: 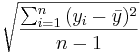 . In ANOVA to describe the combined variation within the k groups we use sums of squares due to error (within-group variation):
. In ANOVA to describe the combined variation within the k groups we use sums of squares due to error (within-group variation):
- SSE(Within) =
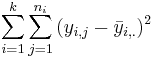 , which can be thought of as the combination of variation within the k groups.
, which can be thought of as the combination of variation within the k groups.
- SSE(within)degrees of freedom: df (Within) = n - k
- Mean variability within groups:
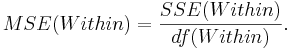 This is a measure of variability within the groups.
This is a measure of variability within the groups.
- Decomposition of Variance: Note that we have the following decomposition of the total variability in the data:
- (Verbal): Deviation of an observation from the grand mean (Total variability) = Variation-Within + Variation_Between!
- (Mathematics):
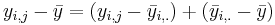 . And summing up over all observations we get the desired ANOVA decomposition.
. And summing up over all observations we get the desired ANOVA decomposition.
- (ANOVA Decomposition):
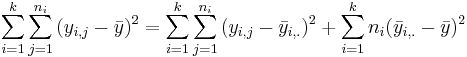 .
.
- Interpretations:
- This means SST(total) = SSE(within) + SST(between)
- df(Total) = df(Within) + df(Between) = (n - k) + (k – 1) = n - 1
SOCR ANOVA Calculations
SOCR Analyses provide the tools to compute the 1-way ANOVA. For example, the ANOVA for the peas data above may be easily computed - see the image below. Note that SOCR ANOVA requires the data to be entered in this format:
| Variety of Pea | ||||
| Value | Group-Index | |||
| 26.2 | A | |||
| 24.3 | A | |||
| 21.8 | A | |||
| 28.1 | A | |||
| 29.2 | B | |||
| 28.1 | B | |||
| 27.3 | B | |||
| 31.2 | B | |||
| 29.1 | C | |||
| 30.8 | C | |||
| 33.9 | C | |||
| 32.8 | C | |||
| 21.3 | D | |||
| 22.4 | D | |||
| 24.3 | D | |||
| 21.8 | D | |||
| 20.1 | E | |||
| 19.3 | E | |||
| 19.9 | E | |||
| 22.1 | E | |||

- F-Value = 23.966
- P-Value = 2.2855121203368967E-6
ANOVA Table
| Variance Source | Degrees of Freedom (df) | Sum of Squares (SS) | Mean Sum of Squares (MS) | F-Statistics | P-value |
| Treatment Effect (Between Group) | k-1 | 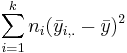 | 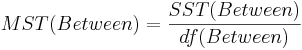 | 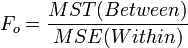 | P(F(df(Between),df(Within)) > Fo) |
| Error (Within Group) | n-k | 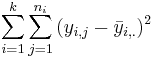 | 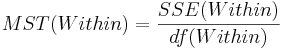 | F-Distribution Calculator | |
| Total | n-1 | 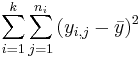 | ANOVA Activity |
ANOVA Hypotheses
The general form of the ANOVA hypotheses is:
-
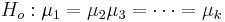
-
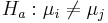 for some
for some 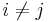 .
.
Note that Ho is compound hypothesis, when k > 2, so rejecting Ho doesn't tell us which μi's are different. It only tells us that some two are not equal.
- Test Statistics: The test statistic:
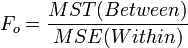 . If Fo is large, then there is a lot of between group variation, relative to the within group variation. Therefore, the discrepancies between the group means are large compared to the variability within the groups (error). Hence, large values of Fo provide strong evidence against Ho.
. If Fo is large, then there is a lot of between group variation, relative to the within group variation. Therefore, the discrepancies between the group means are large compared to the variability within the groups (error). Hence, large values of Fo provide strong evidence against Ho.
Examples
Hands-on Example
This example is provided as a hands-on demonstration of the calculations performed in 1-way ANOVA. Clearly the value added by this example is conceptual understanding and appreciation of the methodological protocol for computing critical values and probabilities in ANOVA designs.
| Groups | |||
| Index | A | B | C |
| 1 | 0 | 1 | 4 |
| 2 | 1 | 0 | 5 |
| 3 | 2 | ||
| ni | 2 | 3 | 2 |
| s | 1 | 3 | 9 |
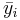 | 0.5 | 1 | 4.5 |
Now use the ANOVA table to calculate the F-statistics and the corresponding p-value. Then use SOCR Analyses (ANOVA) to validate your manual calculations.
| Variance Source | Degrees of Freedom (df) | Sum of Squares (SS) | Mean Sum of Squares (MS) | F-Statistics | P-value |
| Treatment Effect (Between Group) | 3-1 | 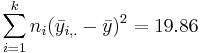 | 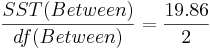 | 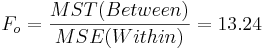 | P(F(df(Between),df(Within)) > Fo) = 0.017 |
| Error (Within Group) | 7-3 | 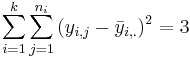 | 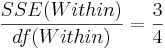 | F-Distribution Calculator | |
| Total | 7-1 | 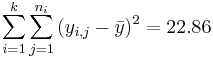 | Anova Activity |
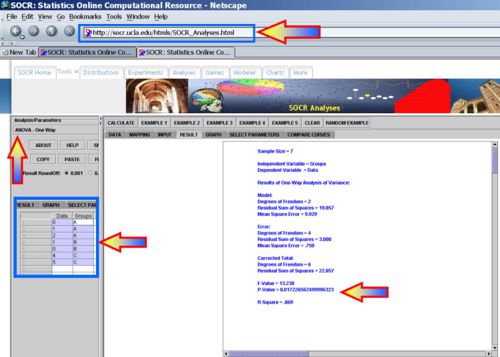
Therefore, in this case we can reject the null hypothesis (at α = 0.05).
Walking Age
Parents are frequently concerned when their child seems slow to begin walking. In 1972, Science reported on an experiment in which the effects of several different treatments on the age at which a child’s first walks were compared. Children in the first group were given special walking exercises for 12 minutes daily beginning at the age 1 week and lasting 7 weeks. The second group of children received daily exercises, but not the walking exercises administered to the first group. The third and forth groups received no special treatment and differed only in that the third group’s progress was checked weekly and the forth was checked only at the end of the study. Observations on age (months) when the child began to walk are on the next slide.
| Age (months) | (Treatment) Group |
| 9 | 1 |
| 9.5 | 1 |
| 9.75 | 1 |
| 10 | 1 |
| 13 | 1 |
| 9.5 | 1 |
| 11 | 2 |
| 10 | 2 |
| 10 | 2 |
| 11.75 | 2 |
| 10.5 | 2 |
| 15 | 2 |
| 11.5 | 3 |
| 12 | 3 |
| 9 | 3 |
| 11.5 | 3 |
| 13.25 | 3 |
| 13 | 3 |
| 13.25 | 4 |
| 11.5 | 4 |
| 12 | 4 |
| 13.5 | 4 |
| 11.5 | 4 |

- Conclusion: These data show that a child's true mean walking age is not statistically significantly different among any of the four treatment groups (p = 0.128546).
ANOVA Conditions
ANOVA is valid if:
- Design conditions: All groups of observations represent random samples from their respective populations. Also required is that the samples, and observations within each group, are independent of one another.
- Population conditions: The k population distributions must be approximately Normal. Normality is less crucial if the sample sizes are large. Also required is that the standard deviations of all populations are equal:
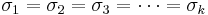 . This condition can be slightly relaxed in practice to
. This condition can be slightly relaxed in practice to 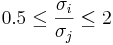 , for all i and j, i.e., none of the population variances is twice larger than any of the other ones.
, for all i and j, i.e., none of the population variances is twice larger than any of the other ones.
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
