AP Statistics Curriculum 2007 ANOVA 2Way
From Socr
(New page: == General Advance-Placement (AP) Statistics Curriculum - Two-Way Analysis of Variance (ANOVA) == === Two-Way ANOVA === Example on how to attach images ...) |
m (→Clinical example: Knee Pain Study) |
||
| (20 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Two-Way Analysis of Variance (ANOVA) == | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Two-Way Analysis of Variance (ANOVA) == | ||
| - | + | In the [[AP_Statistics_Curriculum_2007_ANOVA_1Way |previous section]], we discussed statistical inference in comparing ''k'' independent samples separated by a single (grouping) factor. Now we will discuss variance decomposition of data into (independent/orthogonal) components when we have two (grouping) factors. Hence, this procedure called '''Two-Way Analysis of Variance'''. | |
| - | + | ||
| - | + | ||
| - | === | + | ===Motivational Example=== |
| - | + | Suppose we want to study the dynamics of the [http://en.wikipedia.org/wiki/Consumer_price_index US Consumer Price Index (CPI)], which is a major economic indicator that measures the average price changes of consumer goods and services. | |
| - | + | To motivate 2-way ANOVA we can focus on a 5-year annual summary of the CPI for different types of consumer good (items). The [[SOCR_Data_Dinov_021808_ConsumerPriceIndex2Way | complete dataset can be found here]] and a small 5-year excerpt is included below. Clearly, we have two-factors that may explain the dynamics of the CPI - ''year'' and ''item-type''. | |
| - | === | + | <center> |
| - | + | {| class="wikitable" style="text-align:center; width:30%" border="1" | |
| + | |- | ||
| + | | Year || CPI-Value || Item-Code || Year-Code || Item | ||
| + | |- | ||
| + | | 2003 || 180.5 || 1 || 1 || Food | ||
| + | |- | ||
| + | | 2003 || 184.8 || 2 || 1 || Housing | ||
| + | |- | ||
| + | | 2003 || 157.6 || 3 || 1 || Transportation | ||
| + | |- | ||
| + | | 2003 || 297.1 || 4 || 1 || MedicalCare | ||
| + | |- | ||
| + | | 2004 || 186.6 || 1 || 2 || Food | ||
| + | |- | ||
| + | | 2004 || 189.5 || 2 || 2 || Housing | ||
| + | |- | ||
| + | | 2004 || 163.1 || 3 || 2 || Transportation | ||
| + | |- | ||
| + | | 2004 || 310.1 || 4 || 2 || MedicalCare | ||
| + | |- | ||
| + | | 2005 || 191.2 || 1 || 3 || Food | ||
| + | |- | ||
| + | | 2005 || 195.7 || 2 || 3 || Housing | ||
| + | |- | ||
| + | | 2005 || 173.9 || 3 || 3 || Transportation | ||
| + | |- | ||
| + | | 2005 || 323.2 || 4 || 3 || MedicalCare | ||
| + | |- | ||
| + | | 2006 || 195.7 || 1 || 4 || Food | ||
| + | |- | ||
| + | | 2006 || 203.2 || 2 || 4 || Housing | ||
| + | |- | ||
| + | | 2006 || 180.9 || 3 || 4 || Transportation | ||
| + | |- | ||
| + | | 2006 || 336.2 || 4 || 4 || MedicalCare | ||
| + | |- | ||
| + | | 2007 || 203.3 || 1 || 5 || Food | ||
| + | |- | ||
| + | | 2007 || 209.586 || 2 || 5 || Housing | ||
| + | |- | ||
| + | | 2007 || 184.682 || 3 || 5 || Transportation | ||
| + | |- | ||
| + | | 2007 || 351.054 || 4 || 5 || MedicalCare | ||
| + | |} | ||
| + | <br> | ||
| + | {| class="wikitable" style="text-align:center; width:40%" border="1" | ||
| + | |- | ||
| + | | '''Year''' || '''Food''' || '''Housing''' || '''Transportation''' || '''MedicalCare''' | ||
| + | |- | ||
| + | | 2003 || 180.5 || 184.8 || 157.6 || 297.1 | ||
| + | |- | ||
| + | | 2004 || 186.6 || 189.5 || 163.1 || 310.1 | ||
| + | |- | ||
| + | | 2005 || 191.2 || 195.7 || 173.9 || 323.2 | ||
| + | |- | ||
| + | | 2006 || 195.7 || 203.2 || 180.9 || 336.2 | ||
| + | |- | ||
| + | | 2007 || 203.3 || 209.586 || 184.682 || 351.054 | ||
| + | |} | ||
| + | </center> | ||
| - | + | Using the [http://socr.ucla.edu/htmls/SOCR_Charts.html SOCR Charts] (see [[SOCR_EduMaterials_Activities_BoxAndWhiskerChart | SOCR Box-and-Whisker Plot Activity]] and [[SOCR_EduMaterials_Activities_DotChart | Dot Plot Activity]]), we can generate plots that enable us to compare visually the 4 different CPI items (food, housing, transportation and medical-care) across the 5 years. | |
| - | + | <center>[[Image:SOCR_EBook_Dinov_ANOVA2_022108_Fig1.jpg|500px]]</center> | |
| - | + | ||
| - | + | We can also plot the time courses of these 4 CPI items (using [[SOCR_EduMaterials_Activities_LineChart | the SOCR Line Chart]]. | |
| - | + | ||
| - | + | <center>[[Image:SOCR_EBook_Dinov_ANOVA2_022108_Fig2.jpg|500px]]</center> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | * | + | ===Two-Way ANOVA Calculations=== |
| + | |||
| + | Let's make the following notation: | ||
| + | : Two-way Model: <math>y_{i,j,k} = \mu +\tau_i +\beta_j +\gamma_{i,j} + \epsilon_{i,j,k}</math>, for all <math>1\leq i\leq a</math>, <math>1\leq j\leq b</math> and <math>1\leq k\leq r</math>. Here <math>\mu</math> is the overall mean response, <math>\tau_i</math> is the effect due to the <math>i^{th}</math> level of factor A, <math>\beta_j</math> is the effect due to the <math>j^{th}</math> level of factor B and <math>\gamma_{i,j}</math> is the effect due to any interaction between the <math>i^{th}</math> level of factor A and the <math>j^{th}</math> level of factor B. | ||
| + | |||
| + | : <math>y_{i,j,k}</math> = the A-factor level ''i'' and B-factor level ''j'', ''observation-index k'' measurement. | ||
| + | : k = number of replicates. | ||
| + | : <math>a_i</math> = number of A-factor observations at level ''i'', <math>a= a_1 + a_2 + \cdots + a_I</math>. | ||
| + | : <math>b_j</math> = number of B-factor observations at level ''j'', <math>b= b_1 + b_2 + \cdots + b_J</math>. | ||
| + | : N = total number of observations, <math>N=a\times a \times b</math>. | ||
| + | : The mean of the A-factor group mean at level ''i'' and B-factor at level ''j'' is: <math>\bar{y}_{i,j,.} = {\sum_{k=1}^{r}{y_{i,j,k}} \over r}</math> | ||
| + | : The grand mean is: <math>\bar{y}=\bar{y}_{.,.,.} = {\sum_{k=1}^r{\sum_{i=1}^a {\sum_{j=1}^{b}{y_{i,j,k}}}} \over N}</math>. | ||
| + | |||
| + | When an <math>a \times b</math> factorial experiment is conducted with an equal number of observation per treatment combination, and where AB represents the interaction between A and B, the total (corrected) sum of squares is partitioned as: | ||
| + | |||
| + | <center><math>SS(Total) = SS(A) + SS(B) + SS(AB) + SSE</math></center> | ||
| + | |||
| + | ===Hypotheses=== | ||
| + | There are three sets of hypotheses with the two-way ANOVA. | ||
| + | |||
| + | ====The null hypotheses for each of the sets==== | ||
| + | * The population means of the first factor are equal. This is like the one-way ANOVA for the row factor. | ||
| + | * The population means of the second factor are equal. This is like the one-way ANOVA for the column factor. | ||
| + | * There is no interaction between the two factors. This is similar to performing a test for independence with contingency tables. | ||
| + | |||
| + | ====Factors==== | ||
| + | The two independent variables in a two-way ANOVA are called factors (denoted by A and B). The idea is that there are two variables, factors, which affect the dependent variable (Y). Each factor will have two or more levels within it, and the degrees of freedom for each factor is one less than the number of levels. | ||
| + | |||
| + | ====Treatment Groups==== | ||
| + | Treatment Groups are formed by making all possible combinations of the two factors. For example, if the first factor has 5 levels and the second factor has 6 levels, then there will be <math>5\times6=30</math> different treatment groups. | ||
| + | |||
| + | ====Main Effect==== | ||
| + | The main effect involves the independent variables one at a time. The interaction is ignored for this part. Just the rows or just the columns are used, not mixed. This is the part which is similar to the one-way analysis of variance. Each of the variances calculated to analyze the main effects is like the between variances | ||
| + | |||
| + | ====Interaction Effect==== | ||
| + | The interaction effect is the effect that one factor has on the other factor. The degree of freedom here is the product of the two degrees of freedom for each factor. | ||
| + | |||
| + | ====Within Variation==== | ||
| + | The Within variation is the sum of squares within each treatment group. You have one less than the sample size (remember all treatment groups must have the same sample size for a two-way ANOVA) for each treatment group. The total number of treatment groups is the product of the number of levels for each factor. The within variance is the within variation divided by its degrees of freedom. The within group is also called the error. | ||
| + | |||
| + | ====F-Tests==== | ||
| + | There is an F-test for each of the hypotheses, and the F-test is the mean square for each main effect and the interaction effect divided by the within variance. The numerator degrees of freedom come from each effect, and the denominator degrees of freedom is the degrees of freedom for the within variance in each case. | ||
| + | |||
| + | ====Two-Way ANOVA Table==== | ||
| + | It is assumed that main effect A has ''a'' levels (and df(A) = a-1), main effect B has ''b'' levels (and (df(B) = b-1), ''r'' is the sample size of each treatment, and <math>N = a\times b\times n</math> is the total sample size. Notice the overall degree of freedom is once again one less than the total sample size. | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:50%" border="1" | ||
| + | |- | ||
| + | | Variance Source || Degrees of Freedom (df) || Sum of Squares (SS) || Mean Sum of Squares (MS) || F-Statistics || [http://socr.ucla.edu/htmls/SOCR_Distributions.html P-value] | ||
| + | |- | ||
| + | | Main Effect A || df(A)=a-1 || <math>SS(A)=r\times b\times\sum_{i=1}^{a}{(\bar{y}_{i,.,.}-\bar{y})^2}</math> || <math>{SS(A)\over df(A)}</math> || <math>F_o = {MS(A)\over MSE}</math> || <math>P(F_{(df(A), df(E))} > F_o)</math> | ||
| + | |- | ||
| + | | Main Effect B || df(B)=b-1 || <math>SS(B)=r\times a\times\sum_{j=1}^{b}{(\bar{y}_{., j,.}-\bar{y})^2}</math> || <math>{SS(B)\over df(B)}</math> || <math>F_o = {MS(B)\over MSE}</math> || <math>P(F_{(df(B), df(E))} > F_o)</math> | ||
| + | |- | ||
| + | | A vs.B Interaction || df(AB)=(a-1)(b-1) || <math>SS(AB)=r\times \sum_{i=1}^{a}{\sum_{j=1}^{b}{((\bar{y}_{i, j,.}-\bar{y}_{i, .,.})+(\bar{y}_{., j,.}-\bar{y}))^2}}</math> || <math>{SS(AB)\over df(AB)}</math> || <math>F_o = {MS(AB)\over MSE}</math> || <math>P(F_{(df(AB), df(E))} > F_o)</math> | ||
| + | |- | ||
| + | | Error || <math>N-a\times b</math> || <math>SSE=\sum_{k=1}^r{\sum_{i=1}^{a}{\sum_{j=1}^{b}{(\bar{y}_{i, j,k}-\bar{y}_{i, j,.})^2}}}</math> || <math>{SSE\over df(Error)}</math> || || | ||
| + | |- | ||
| + | | Total || N-1 || <math>SST=\sum_{k=1}^r{\sum_{i=1}^{a}{\sum_{j=1}^{b}{(\bar{y}_{i, j,k}-\bar{y}_{., .,.})^2}}}</math> || || || [[SOCR_EduMaterials_AnalysisActivities_ANOVA_2 | ANOVA Activity]] | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | To compute the difference between the means, we will compare each group mean to the grand mean. | ||
| + | |||
| + | ===SOCR ANOVA Calculations=== | ||
| + | [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] provide the tools to compute the [[SOCR_EduMaterials_AnalysisActivities_ANOVA_2 |2-way ANOVA]]. For example, the ANOVA for the Consumer Price Index data above may be easily computed - see the image below. Note that SOCR ANOVA requires the data to be entered in the [[AP_Statistics_Curriculum_2007_ANOVA_2Way#Motivational_Example | column format of the first table in this section]]. | ||
| + | |||
| + | <center>[[Image:SOCR_EBook_Dinov_ANOVA2_022108_Fig3.jpg|500px]]</center> | ||
| + | |||
| + | Under the '''Graphs''' tab-pane, we can see a variety of plots demonstrating the ANOVA results. | ||
| + | |||
| + | <center>[[Image:SOCR_EBook_Dinov_ANOVA2_022108_Fig4.jpg|500px]]</center> | ||
| + | |||
| + | The ANOVA table for these data is reported under the '''Results''' tab-pane. | ||
| + | |||
| + | |||
| + | ::Sample Size = 20 | ||
| + | ::Dependent Variable = CPI-Value | ||
| + | ::Independent Variable(s) = Year Item | ||
| + | |||
| + | ::--- Two-Way Analysis of Variance Results --- | ||
| + | |||
| + | ::'''Variable: Year''' | ||
| + | ::Degrees of Freedom = 4 | ||
| + | ::Residual Sum of Squares = 2624.8073168000 | ||
| + | ::Mean Square Error = 656.2018292000 | ||
| + | ::F-Value = 19.3405175758 | ||
| + | ::P-Value = .0000363212 | ||
| + | |||
| + | ::'''Variable: Item''' | ||
| + | ::Degrees of Freedom = 3 | ||
| + | ::Residual Sum of Squares = 71900.0898230001 | ||
| + | ::Mean Square Error = 23966.6966076667 | ||
| + | ::F-Value = 706.3807145121 | ||
| + | ::P-Value = .0000000000 | ||
| + | |||
| + | ::Residual: Degrees of Freedom = 12 | ||
| + | ::Residual Sum of Squares = 407.1463920000 | ||
| + | ::Mean Square Error = 33.9288660000 | ||
| + | ::F-Value = 322.4822657900 | ||
| + | ::P-Value = 0.0 | ||
| + | |||
| + | ::R-Square = .9945664582 | ||
| + | |||
| + | ===Two-Way ANOVA Conditions=== | ||
| + | The Two-way ANOVA is valid if: | ||
| + | * The populations from which the samples were obtained must be normally or approximately normally distributed. | ||
| + | * The samples must be independent. | ||
| + | * The variances of the populations must be equal. | ||
| + | * The groups must have the same sample size. | ||
| + | |||
| + | ===Clinical example: Knee Pain Study=== | ||
| + | The following data was collected in a large knee pain study ('''N=6,046''') by [http://www.masterdocs.com TMT Medical] and [http://socr.ucla.edu/ UCLA] investigators using an [https://www.masterdocs.com/kneepain/start.php online questionnaire]. The goals of the study was to identify the relations between a large number of clinical markers, patient phenotypes and imaging data of knee pain. One specific set of research questions the investigators were interested in related to the effects of mild treatment by applying hot or cold patches to the affected knee areas. The 2 tables below present identical information, however, the second table may be used to paste in the data into the [http://www.socr.ucla.edu/htmls/ana/ANOVA2Way_Analysis.html SOCR 2-way ANOVA Applet] or any other [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR analysis tool]. Try to answer 2 types of questions: | ||
| + | * Are there significant effects of the type-of-diagnosis ('''DiagnosisType''') and/or the type-of-treatment ('''TreatmentType(Cold=1_Hot=2)''') on the observed frequencies of reported benefits? | ||
| + | * Are there interactions between the type-of-diagnosis and the type-of-treatment? | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Diagnosis || RespondersToColdTreatment || RespondersToHotTreatment || NoResponseToHotOrColdTreatment || Total | ||
| + | |- | ||
| + | | A_Bursitis || 18 || 3 || 32 || 53 | ||
| + | |- | ||
| + | | I_Bursitis || 14 || 1 || 13 || 28 | ||
| + | |- | ||
| + | | P_Bursitis || 33 || 17 || 78 || 128 | ||
| + | |- | ||
| + | | LCL_Injury || 10 || 6 || 39 || 55 | ||
| + | |- | ||
| + | | MCL_Injury || 56 || 22 || 95 || 173 | ||
| + | |- | ||
| + | | PCL_Injury || 6 || 4 || 17 || 27 | ||
| + | |- | ||
| + | | Bakers_Cyst || 28 || 15 || 91 || 134 | ||
| + | |- | ||
| + | | Chondromalacia || 290 || 90 || 478 || 858 | ||
| + | |- | ||
| + | | Dislocation || 37 || 8 || 102 || 147 | ||
| + | |- | ||
| + | | IBS || 173 || 29 || 262 || 464 | ||
| + | |- | ||
| + | | Lateral_Meniscus || 49 || 10 || 110 || 169 | ||
| + | |- | ||
| + | | Medial_Meniscus || 147 || 35 || 277 || 459 | ||
| + | |- | ||
| + | | Osteoarthritis || 442 || 290 || 1478 || 2210 | ||
| + | |- | ||
| + | | Other || 102 || 57 || 337 || 496 | ||
| + | |- | ||
| + | | Plica_Syndrome || 24 || 9 || 33 || 66 | ||
| + | |- | ||
| + | | Rheumatoid_Arthritis || 25 || 19 || 115 || 159 | ||
| + | |- | ||
| + | | Tendon_Tear || 25 || 7 || 61 || 93 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! ClinicalDiagnosis || DiagnosisType || TreatmentType(Cold=1_Hot=2) || NumberOfRespondersToTreatment | ||
| + | |- | ||
| + | | ACL_Injury || Acute_Injury || 1 || 110 | ||
| + | |- | ||
| + | | Dislocation || Acute_Injury || 1 || 37 | ||
| + | |- | ||
| + | | Lateral_Meniscus || Acute_Injury || 1 || 49 | ||
| + | |- | ||
| + | | LCL_Injury || Acute_Injury || 1 || 10 | ||
| + | |- | ||
| + | | MCL_Injury || Acute_Injury || 1 || 56 | ||
| + | |- | ||
| + | | Medial_Meniscus || Acute_Injury || 1 || 147 | ||
| + | |- | ||
| + | | PCL_Injury || Acute_Injury || 1 || 6 | ||
| + | |- | ||
| + | | Tendon_Tear || Acute_Injury || 1 || 25 | ||
| + | |- | ||
| + | | Osteoarthritis || Arthritis || 1 || 442 | ||
| + | |- | ||
| + | | Rheumatoid_Arthritis || Arthritis || 1 || 25 | ||
| + | |- | ||
| + | | A_Bursitis || Bursitis || 1 || 18 | ||
| + | |- | ||
| + | | I_Bursitis || Bursitis || 1 || 14 | ||
| + | |- | ||
| + | | P_Bursitis || Bursitis || 1 || 33 | ||
| + | |- | ||
| + | | Plica_Syndrome || Other || 1 || 24 | ||
| + | |- | ||
| + | | Chondromalacia || Overuse || 1 || 290 | ||
| + | |- | ||
| + | | IBS || Overuse || 1 || 173 | ||
| + | |- | ||
| + | | Bakers_Cyst || Other || 1 || 28 | ||
| + | |- | ||
| + | | Other || Other || 1 || 102 | ||
| + | |- | ||
| + | | ACL_Injury || Acute_Injury || 2 || 18 | ||
| + | |- | ||
| + | | Dislocation || Acute_Injury || 2 || 8 | ||
| + | |- | ||
| + | | Lateral_Meniscus || Acute_Injury || 2 || 10 | ||
| + | |- | ||
| + | | LCL_Injury || Acute_Injury || 2 || 6 | ||
| + | |- | ||
| + | | MCL_Injury || Acute_Injury || 2 || 22 | ||
| + | |- | ||
| + | | Medial_Meniscus || Acute_Injury || 2 || 35 | ||
| + | |- | ||
| + | | PCL_Injury || Acute_Injury || 2 || 4 | ||
| + | |- | ||
| + | | Tendon_Tear || Acute_Injury || 2 || 7 | ||
| + | |- | ||
| + | | Osteoarthritis || Arthritis || 2 || 290 | ||
| + | |- | ||
| + | | Rheumatoid_Arthritis || Arthritis || 2 || 19 | ||
| + | |- | ||
| + | | A_Bursitis || Bursitis || 2 || 3 | ||
| + | |- | ||
| + | | I_Bursitis || Bursitis || 2 || 1 | ||
| + | |- | ||
| + | | P_Bursitis || Bursitis || 2 || 17 | ||
| + | |- | ||
| + | | Plica_Syndrome || Other || 2 || 9 | ||
| + | |- | ||
| + | | Chondromalacia || Overuse || 2 || 90 | ||
| + | |- | ||
| + | | IBS || Overuse || 2 || 29 | ||
| + | |- | ||
| + | | Bakers_Cyst || Other || 2 || 15 | ||
| + | |- | ||
| + | | Other || Other || 2 || 57 | ||
| + | |} | ||
| + | </center> | ||
<hr> | <hr> | ||
| - | === | + | |
| - | + | ===[[Ebook_Problems_ANOVA_2Way|Problems]]=== | |
<hr> | <hr> | ||
Current revision as of 19:30, 6 October 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Two-Way Analysis of Variance (ANOVA)
In the previous section, we discussed statistical inference in comparing k independent samples separated by a single (grouping) factor. Now we will discuss variance decomposition of data into (independent/orthogonal) components when we have two (grouping) factors. Hence, this procedure called Two-Way Analysis of Variance.
Motivational Example
Suppose we want to study the dynamics of the US Consumer Price Index (CPI), which is a major economic indicator that measures the average price changes of consumer goods and services.
To motivate 2-way ANOVA we can focus on a 5-year annual summary of the CPI for different types of consumer good (items). The complete dataset can be found here and a small 5-year excerpt is included below. Clearly, we have two-factors that may explain the dynamics of the CPI - year and item-type.
| Year | CPI-Value | Item-Code | Year-Code | Item |
| 2003 | 180.5 | 1 | 1 | Food |
| 2003 | 184.8 | 2 | 1 | Housing |
| 2003 | 157.6 | 3 | 1 | Transportation |
| 2003 | 297.1 | 4 | 1 | MedicalCare |
| 2004 | 186.6 | 1 | 2 | Food |
| 2004 | 189.5 | 2 | 2 | Housing |
| 2004 | 163.1 | 3 | 2 | Transportation |
| 2004 | 310.1 | 4 | 2 | MedicalCare |
| 2005 | 191.2 | 1 | 3 | Food |
| 2005 | 195.7 | 2 | 3 | Housing |
| 2005 | 173.9 | 3 | 3 | Transportation |
| 2005 | 323.2 | 4 | 3 | MedicalCare |
| 2006 | 195.7 | 1 | 4 | Food |
| 2006 | 203.2 | 2 | 4 | Housing |
| 2006 | 180.9 | 3 | 4 | Transportation |
| 2006 | 336.2 | 4 | 4 | MedicalCare |
| 2007 | 203.3 | 1 | 5 | Food |
| 2007 | 209.586 | 2 | 5 | Housing |
| 2007 | 184.682 | 3 | 5 | Transportation |
| 2007 | 351.054 | 4 | 5 | MedicalCare |
| Year | Food | Housing | Transportation | MedicalCare |
| 2003 | 180.5 | 184.8 | 157.6 | 297.1 |
| 2004 | 186.6 | 189.5 | 163.1 | 310.1 |
| 2005 | 191.2 | 195.7 | 173.9 | 323.2 |
| 2006 | 195.7 | 203.2 | 180.9 | 336.2 |
| 2007 | 203.3 | 209.586 | 184.682 | 351.054 |
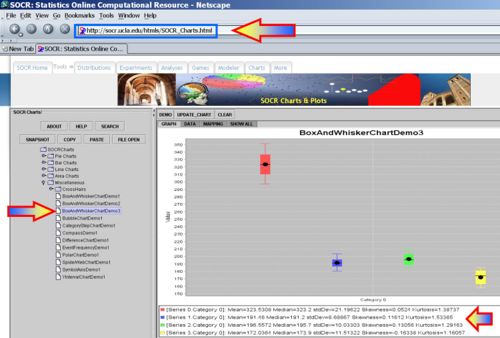
Using the SOCR Charts (see SOCR Box-and-Whisker Plot Activity and Dot Plot Activity), we can generate plots that enable us to compare visually the 4 different CPI items (food, housing, transportation and medical-care) across the 5 years.
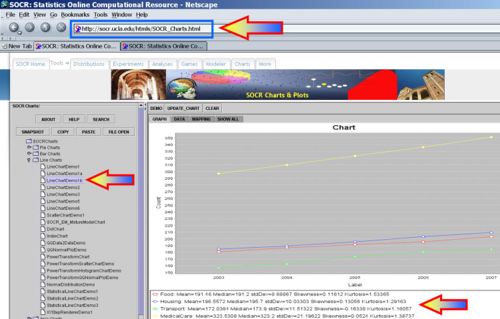
We can also plot the time courses of these 4 CPI items (using the SOCR Line Chart.
Two-Way ANOVA Calculations
Let's make the following notation:
- Two-way Model: yi,j,k = μ + τi + βj + γi,j + εi,j,k, for all
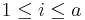 ,
, 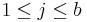 and
and 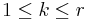 . Here μ is the overall mean response, τi is the effect due to the ith level of factor A, βj is the effect due to the jth level of factor B and γi,j is the effect due to any interaction between the ith level of factor A and the jth level of factor B.
. Here μ is the overall mean response, τi is the effect due to the ith level of factor A, βj is the effect due to the jth level of factor B and γi,j is the effect due to any interaction between the ith level of factor A and the jth level of factor B.
- yi,j,k = the A-factor level i and B-factor level j, observation-index k measurement.
- k = number of replicates.
- ai = number of A-factor observations at level i,
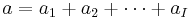 .
.
- bj = number of B-factor observations at level j,
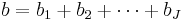 .
.
- N = total number of observations,
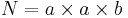 .
.
- The mean of the A-factor group mean at level i and B-factor at level j is:
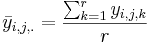
- The grand mean is:
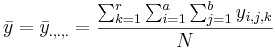 .
.
When an  factorial experiment is conducted with an equal number of observation per treatment combination, and where AB represents the interaction between A and B, the total (corrected) sum of squares is partitioned as:
factorial experiment is conducted with an equal number of observation per treatment combination, and where AB represents the interaction between A and B, the total (corrected) sum of squares is partitioned as:
Hypotheses
There are three sets of hypotheses with the two-way ANOVA.
The null hypotheses for each of the sets
- The population means of the first factor are equal. This is like the one-way ANOVA for the row factor.
- The population means of the second factor are equal. This is like the one-way ANOVA for the column factor.
- There is no interaction between the two factors. This is similar to performing a test for independence with contingency tables.
Factors
The two independent variables in a two-way ANOVA are called factors (denoted by A and B). The idea is that there are two variables, factors, which affect the dependent variable (Y). Each factor will have two or more levels within it, and the degrees of freedom for each factor is one less than the number of levels.
Treatment Groups
Treatment Groups are formed by making all possible combinations of the two factors. For example, if the first factor has 5 levels and the second factor has 6 levels, then there will be 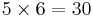 different treatment groups.
different treatment groups.
Main Effect
The main effect involves the independent variables one at a time. The interaction is ignored for this part. Just the rows or just the columns are used, not mixed. This is the part which is similar to the one-way analysis of variance. Each of the variances calculated to analyze the main effects is like the between variances
Interaction Effect
The interaction effect is the effect that one factor has on the other factor. The degree of freedom here is the product of the two degrees of freedom for each factor.
Within Variation
The Within variation is the sum of squares within each treatment group. You have one less than the sample size (remember all treatment groups must have the same sample size for a two-way ANOVA) for each treatment group. The total number of treatment groups is the product of the number of levels for each factor. The within variance is the within variation divided by its degrees of freedom. The within group is also called the error.
F-Tests
There is an F-test for each of the hypotheses, and the F-test is the mean square for each main effect and the interaction effect divided by the within variance. The numerator degrees of freedom come from each effect, and the denominator degrees of freedom is the degrees of freedom for the within variance in each case.
Two-Way ANOVA Table
It is assumed that main effect A has a levels (and df(A) = a-1), main effect B has b levels (and (df(B) = b-1), r is the sample size of each treatment, and 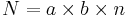 is the total sample size. Notice the overall degree of freedom is once again one less than the total sample size.
is the total sample size. Notice the overall degree of freedom is once again one less than the total sample size.
| Variance Source | Degrees of Freedom (df) | Sum of Squares (SS) | Mean Sum of Squares (MS) | F-Statistics | P-value |
| Main Effect A | df(A)=a-1 | 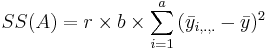 | 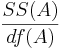 | 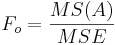 | P(F(df(A),df(E)) > Fo) |
| Main Effect B | df(B)=b-1 | 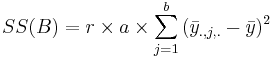 | 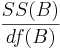 | 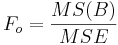 | P(F(df(B),df(E)) > Fo) |
| A vs.B Interaction | df(AB)=(a-1)(b-1) | 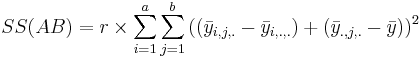 | 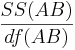 | 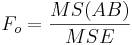 | P(F(df(AB),df(E)) > Fo) |
| Error | 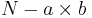 | 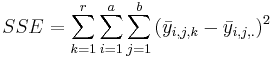 | 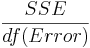 | ||
| Total | N-1 | 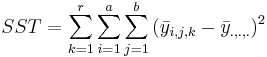 | ANOVA Activity |
To compute the difference between the means, we will compare each group mean to the grand mean.
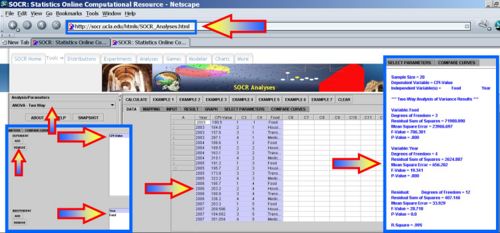
SOCR ANOVA Calculations
SOCR Analyses provide the tools to compute the 2-way ANOVA. For example, the ANOVA for the Consumer Price Index data above may be easily computed - see the image below. Note that SOCR ANOVA requires the data to be entered in the column format of the first table in this section.
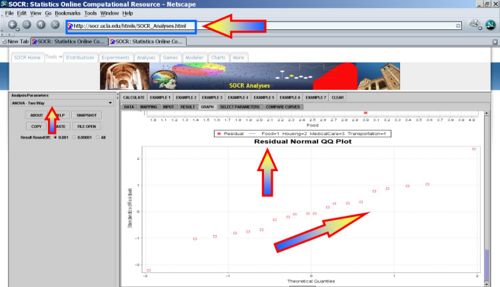
Under the Graphs tab-pane, we can see a variety of plots demonstrating the ANOVA results.
The ANOVA table for these data is reported under the Results tab-pane.
- Sample Size = 20
- Dependent Variable = CPI-Value
- Independent Variable(s) = Year Item
- --- Two-Way Analysis of Variance Results ---
- Variable: Year
- Degrees of Freedom = 4
- Residual Sum of Squares = 2624.8073168000
- Mean Square Error = 656.2018292000
- F-Value = 19.3405175758
- P-Value = .0000363212
- Variable: Item
- Degrees of Freedom = 3
- Residual Sum of Squares = 71900.0898230001
- Mean Square Error = 23966.6966076667
- F-Value = 706.3807145121
- P-Value = .0000000000
- Residual: Degrees of Freedom = 12
- Residual Sum of Squares = 407.1463920000
- Mean Square Error = 33.9288660000
- F-Value = 322.4822657900
- P-Value = 0.0
- R-Square = .9945664582
Two-Way ANOVA Conditions
The Two-way ANOVA is valid if:
- The populations from which the samples were obtained must be normally or approximately normally distributed.
- The samples must be independent.
- The variances of the populations must be equal.
- The groups must have the same sample size.
Clinical example: Knee Pain Study
The following data was collected in a large knee pain study (N=6,046) by TMT Medical and UCLA investigators using an online questionnaire. The goals of the study was to identify the relations between a large number of clinical markers, patient phenotypes and imaging data of knee pain. One specific set of research questions the investigators were interested in related to the effects of mild treatment by applying hot or cold patches to the affected knee areas. The 2 tables below present identical information, however, the second table may be used to paste in the data into the SOCR 2-way ANOVA Applet or any other SOCR analysis tool. Try to answer 2 types of questions:
- Are there significant effects of the type-of-diagnosis (DiagnosisType) and/or the type-of-treatment (TreatmentType(Cold=1_Hot=2)) on the observed frequencies of reported benefits?
- Are there interactions between the type-of-diagnosis and the type-of-treatment?
| Diagnosis | RespondersToColdTreatment | RespondersToHotTreatment | NoResponseToHotOrColdTreatment | Total |
|---|---|---|---|---|
| A_Bursitis | 18 | 3 | 32 | 53 |
| I_Bursitis | 14 | 1 | 13 | 28 |
| P_Bursitis | 33 | 17 | 78 | 128 |
| LCL_Injury | 10 | 6 | 39 | 55 |
| MCL_Injury | 56 | 22 | 95 | 173 |
| PCL_Injury | 6 | 4 | 17 | 27 |
| Bakers_Cyst | 28 | 15 | 91 | 134 |
| Chondromalacia | 290 | 90 | 478 | 858 |
| Dislocation | 37 | 8 | 102 | 147 |
| IBS | 173 | 29 | 262 | 464 |
| Lateral_Meniscus | 49 | 10 | 110 | 169 |
| Medial_Meniscus | 147 | 35 | 277 | 459 |
| Osteoarthritis | 442 | 290 | 1478 | 2210 |
| Other | 102 | 57 | 337 | 496 |
| Plica_Syndrome | 24 | 9 | 33 | 66 |
| Rheumatoid_Arthritis | 25 | 19 | 115 | 159 |
| Tendon_Tear | 25 | 7 | 61 | 93 |
| ClinicalDiagnosis | DiagnosisType | TreatmentType(Cold=1_Hot=2) | NumberOfRespondersToTreatment |
|---|---|---|---|
| ACL_Injury | Acute_Injury | 1 | 110 |
| Dislocation | Acute_Injury | 1 | 37 |
| Lateral_Meniscus | Acute_Injury | 1 | 49 |
| LCL_Injury | Acute_Injury | 1 | 10 |
| MCL_Injury | Acute_Injury | 1 | 56 |
| Medial_Meniscus | Acute_Injury | 1 | 147 |
| PCL_Injury | Acute_Injury | 1 | 6 |
| Tendon_Tear | Acute_Injury | 1 | 25 |
| Osteoarthritis | Arthritis | 1 | 442 |
| Rheumatoid_Arthritis | Arthritis | 1 | 25 |
| A_Bursitis | Bursitis | 1 | 18 |
| I_Bursitis | Bursitis | 1 | 14 |
| P_Bursitis | Bursitis | 1 | 33 |
| Plica_Syndrome | Other | 1 | 24 |
| Chondromalacia | Overuse | 1 | 290 |
| IBS | Overuse | 1 | 173 |
| Bakers_Cyst | Other | 1 | 28 |
| Other | Other | 1 | 102 |
| ACL_Injury | Acute_Injury | 2 | 18 |
| Dislocation | Acute_Injury | 2 | 8 |
| Lateral_Meniscus | Acute_Injury | 2 | 10 |
| LCL_Injury | Acute_Injury | 2 | 6 |
| MCL_Injury | Acute_Injury | 2 | 22 |
| Medial_Meniscus | Acute_Injury | 2 | 35 |
| PCL_Injury | Acute_Injury | 2 | 4 |
| Tendon_Tear | Acute_Injury | 2 | 7 |
| Osteoarthritis | Arthritis | 2 | 290 |
| Rheumatoid_Arthritis | Arthritis | 2 | 19 |
| A_Bursitis | Bursitis | 2 | 3 |
| I_Bursitis | Bursitis | 2 | 1 |
| P_Bursitis | Bursitis | 2 | 17 |
| Plica_Syndrome | Other | 2 | 9 |
| Chondromalacia | Overuse | 2 | 90 |
| IBS | Overuse | 2 | 29 |
| Bakers_Cyst | Other | 2 | 15 |
| Other | Other | 2 | 57 |
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
