AP Statistics Curriculum 2007 Bayesian Normal
From Socr
(New page: ''Normal Example:'' It is known that the speedometer that comes with a certain new sports car is not very accurate, which results in an estimate of the top speed of the car of 185 mph, wi...) |
(→Motivational example) |
||
| (11 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | ==[[EBook | Probability and Statistics Ebook]] - Normal Example== | |
| - | It is known that the speedometer that comes with a certain new sports car is not very accurate, which results in an estimate of the top speed of the car of 185 mph, with a standard deviation of 10 mph. Knowing that his car is capable of much higher speeds, the owner | + | ===Motivational example=== |
| - | + | It is known that the speedometer that comes with a certain new sports car is not very accurate, which results in an estimate of the top speed of the car of 185 mph, with a standard deviation of 10 mph. Knowing that his car is capable of much higher speeds, the owner take the car to the shop. After a checkup, the speedometer is replaced with a better one, which gives a new estimate of 220 mph with a standard deviation of 4 mph. The errors are assumed to be normally distributed. | |
| - | + | We can say that the owner '''S’s''' prior beliefs about the top speed of his car are represented by: | |
| + | |||
| + | : <math>\mu \sim N \mu_0</math>, <math>\phi_0</math>, i.e., <math>\mu \sim N(185,10^2)</math> | ||
We could then say that the measurements using the new speedometer result in a measurement of: | We could then say that the measurements using the new speedometer result in a measurement of: | ||
| - | + | :<math>x \sim N(\mu, \phi)</math>, i.e., <math> x \sim N(\mu, 4^2)</math> | |
| - | We note that the observation '''x''' turned out to be 210, and we see that S’s posterior beliefs about '''µ''' should be represented by: | + | We note that the observation '''x''' turned out to be 210, and we see that '''S’s''' posterior beliefs about '''µ''' should be represented by: |
| - | < | + | :<math>\mu | x \sim N(\mu_1, \phi_1)</math> |
where (rounded) | where (rounded) | ||
| - | + | :<math>\phi_1 = (10^{-2} + 4^{-2})^{-1} = 14 = 4^2</math> | |
| - | + | :<math>\mu_1 = 14(185/10^2 + 220/4^2) = 218</math>. | |
Therefore, the posterior for the top speed is: | Therefore, the posterior for the top speed is: | ||
| - | + | :<math>\mu | x \sim N(218,4^2)</math>. Meaning 218 +/- 4 mph. | |
| - | + | If the new speedometer measurements were considered by another person '''S’''' who had no knowledge of the readings from the first speedometer, but still had a vague idea (from knowledge of the stock speedometer) that the top speed was about 200 +/- 30 mph. Then: | |
| - | + | :<math>\mu \sim N(200,30^2)</math>. | |
| - | + | ||
| - | + | ||
| - | + | ||
Then '''S’''' would have a posterior variance: | Then '''S’''' would have a posterior variance: | ||
| - | + | : <math>\phi_1 = (30^{-2} + 4^{-2})^{-1} = 16 = 4^2</math>. | |
'''S’''' would have a posterior mean of: | '''S’''' would have a posterior mean of: | ||
| + | |||
| + | :<math>\mu_1 = 16(200/30^2 + 220/4^2) = 224</math>. | ||
| + | |||
| + | Therefore, the distribution of '''S’''' would be: | ||
| + | |||
| + | :<math>\mu | x \sim N(224,4^2)</math>. Meaning 224 +/- 4 mph. | ||
| + | |||
| + | This calculation has been carried out assuming that the prior information we have is rather vague, and therefore the posterior is almost entirely determined by the data. | ||
| + | |||
| + | The situation is summarized as follows: | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:25%" border="1" | ||
| + | |- | ||
| + | ! Speed || Prior Distribution || Likelihood from Data || Posterior Distribution | ||
| + | |- | ||
| + | | S || <math>N(185 , 10^2)</math> || || <math>N(218 , 4^2)</math> | ||
| + | |- | ||
| + | |- | ||
| + | | || || <math>N(220 , 4^2)</math> || | ||
| + | |- | ||
| + | | S’ || <math>N(200,30^2)</math>|| || <math>N(224,4^2)</math> | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | ==See also== | ||
| + | * [[EBook#Chapter_III:_Probability |Probability Chapter]] | ||
| + | |||
| + | ==References== | ||
| + | |||
| + | <hr> | ||
| + | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | |||
| + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=AP_Statistics_Curriculum_2007_Bayesian_Normal}} | ||
Current revision as of 21:09, 28 June 2010
Contents |
Probability and Statistics Ebook - Normal Example
Motivational example
It is known that the speedometer that comes with a certain new sports car is not very accurate, which results in an estimate of the top speed of the car of 185 mph, with a standard deviation of 10 mph. Knowing that his car is capable of much higher speeds, the owner take the car to the shop. After a checkup, the speedometer is replaced with a better one, which gives a new estimate of 220 mph with a standard deviation of 4 mph. The errors are assumed to be normally distributed.
We can say that the owner S’s prior beliefs about the top speed of his car are represented by:
-
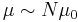 , φ0, i.e.,
, φ0, i.e., 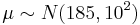
We could then say that the measurements using the new speedometer result in a measurement of:
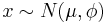 , i.e.,
, i.e., 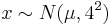
We note that the observation x turned out to be 210, and we see that S’s posterior beliefs about µ should be represented by:
where (rounded)
- φ1 = (10 − 2 + 4 − 2) − 1 = 14 = 42
- μ1 = 14(185 / 102 + 220 / 42) = 218.
Therefore, the posterior for the top speed is:
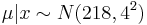 . Meaning 218 +/- 4 mph.
. Meaning 218 +/- 4 mph.
If the new speedometer measurements were considered by another person S’ who had no knowledge of the readings from the first speedometer, but still had a vague idea (from knowledge of the stock speedometer) that the top speed was about 200 +/- 30 mph. Then:
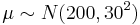 .
.
Then S’ would have a posterior variance:
- φ1 = (30 − 2 + 4 − 2) − 1 = 16 = 42.
S’ would have a posterior mean of:
- μ1 = 16(200 / 302 + 220 / 42) = 224.
Therefore, the distribution of S’ would be:
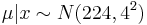 . Meaning 224 +/- 4 mph.
. Meaning 224 +/- 4 mph.
This calculation has been carried out assuming that the prior information we have is rather vague, and therefore the posterior is almost entirely determined by the data.
The situation is summarized as follows:
| Speed | Prior Distribution | Likelihood from Data | Posterior Distribution |
|---|---|---|---|
| S | N(185,102) | N(218,42) | |
| N(220,42) | |||
| S’ | N(200,302) | N(224,42) |
See also
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: