AP Statistics Curriculum 2007 Bayesian Other
From Socr
| Line 26: | Line 26: | ||
(P|x) ~ β(α + x, β + n – x) | (P|x) ~ β(α + x, β + n – x) | ||
| + | |||
| + | |||
| + | |||
| + | '''Bayesian Inference for the Poisson Distribution''' | ||
| + | |||
| + | A discrete random variable x is said to have a Poisson distribution of mean <math>\lambda</math> if it has the density | ||
| + | |||
| + | |||
| + | P(x|<math>\lambda</math>) = (<math>\lambda^x</x!</math>)<math>e^{-\lambda}</math> | ||
| + | |||
| + | Supose that you have n observations x=(x1, x2, …, xn) from such a distribution so that the likelihood is | ||
| + | |||
| + | |||
| + | L(<math>\lambda</math>|x) = <math>\lambda^T e^{(-n \lambda)}</math>, where T = <math>\sum{k_i}</math> | ||
| + | |||
| + | In Bayesian inference, the conjugate prior for the parameter <math>\lambda</math> of the Poisson distribution is the Gamma distribution. | ||
| + | |||
| + | <math>\lambda \sim</math> Gamma(<math>\alpha</math> , <math>\beta</math> ) | ||
| + | |||
| + | |||
| + | The Poisson parameter <math>\lambda</math> is distributed accordingly to the parameterized Gamma density g in terms of a shape and inverse scale parameter <math>\alpha</math> and <math>\beta</math> respectively | ||
| + | |||
| + | |||
| + | g(<math>\lambda</math>|<math>\alpha</math> , <math>\beta</math>) = <math>\displaystyle\frac{\beta^\alpha}{\Gamma(\alpha)}</math> <math>\lambda^{\alpha - 1} e^{-\beta \lambda}</math> | ||
| + | For <math>\lambda</math> > 0 | ||
| + | |||
| + | |||
| + | Then, given the same sample of n measured values <math>k_i</math> from our likelihood and a prior of Gamma(<math>\alpha</math>, <math>\beta</math>), the posterior distribution becomes | ||
| + | |||
| + | |||
| + | <math>\lambda \sim</math> Gamma (<math>\alpha + \displaystyle\sum_{i=1}^{\infty} k_i</math> , <math>\beta</math> + n) | ||
| + | |||
| + | The posterior mean E[<math>\lambda</math>] approaches the maximum likelihood estimate in the limit as <math>\alpha</math> and <math>\beta</math> approach 0. | ||
Revision as of 06:34, 2 June 2009
Bayesian Inference for the Binomial Distribution
The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a binomial distribution of index n and parameter P
x ~ B(n,P)
subsequently, we can show that
p(x|P) = 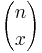 Px (1 − P)n − x , (x = 0, 1, …, n)
Px (1 − P)n − x , (x = 0, 1, …, n)
p(x|P) is proportional to Px(1 − P)n − x
If the prior density has the form:
p(P) proportional to Pα − 1(P − 1)β − 1 , (P between 0 and 1)
then it follows the beta distribution P ~ β(α,β)
From this we can appropriate the posterior which evidently has the form
p(P|x) is proportional to Pα + x − 1(1 − P)β + n − x − 1
The posterior distribution of the Binomial is
(P|x) ~ β(α + x, β + n – x)
Bayesian Inference for the Poisson Distribution
A discrete random variable x is said to have a Poisson distribution of mean λ if it has the density
P(x|λ) = (λx < / x!)e − λ
Supose that you have n observations x=(x1, x2, …, xn) from such a distribution so that the likelihood is
L(λ|x) = λTe( − nλ), where T = 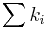
In Bayesian inference, the conjugate prior for the parameter λ of the Poisson distribution is the Gamma distribution.
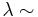 Gamma(α , β )
Gamma(α , β )
The Poisson parameter λ is distributed accordingly to the parameterized Gamma density g in terms of a shape and inverse scale parameter α and β respectively
g(λ|α , β) = 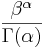 λα − 1e − βλ
For λ > 0
λα − 1e − βλ
For λ > 0
Then, given the same sample of n measured values ki from our likelihood and a prior of Gamma(α, β), the posterior distribution becomes
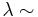 Gamma (
Gamma (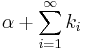 , β + n)
, β + n)
The posterior mean E[λ] approaches the maximum likelihood estimate in the limit as α and β approach 0.
