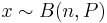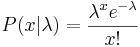AP Statistics Curriculum 2007 Bayesian Other
From Socr
m (→Probability and Statistics Ebook - Bayesian Inference for the Binomial and Poisson Distributions) |
|||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| - | + | ==[[EBook | Probability and Statistics Ebook]] - Bayesian Inference for the Binomial and Poisson Distributions== | |
| - | + | ||
| - | The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a binomial distribution of index n and parameter P | + | The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a [[EBook#Bernoulli_and_Binomial_Experiments |binomial distribution of index n and parameter P]]: |
| + | : <math>x \sim B(n,P)</math> | ||
| - | + | We can show that | |
| - | + | : <math>p(x|P) = {n \choose x} P^x (1 - P)^{n - x}</math>, (x = 0, 1, …, n) | |
| - | + | ||
| - | p(x|P) = | + | |
| - | + | ||
| - | + | ||
| + | : p(x|P) is proportional to <math>P^x (1 - P)^{n - x}</math>. | ||
If the prior density has the form: | If the prior density has the form: | ||
| - | p(P) | + | : <math>p(P) \sim P^{\alpha - 1} (P-1)^{\beta - 1}</math>, (P between 0 and 1), |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | then it follows the [http://socr.ucla.edu/htmls/dist/Beta_Distribution.html beta distribution] | ||
| + | : <math>P \sim \beta(\alpha,\beta)</math>. | ||
| - | + | From this we can appropriate the posterior which evidently has the form: | |
| + | : <math>p(P|x) \sim P^{\alpha + x - 1} (1-P)^{\beta + n - x - 1}</math>. | ||
| - | + | The posterior distribution of the [[EBook#Bernoulli_and_Binomial_Experiments |Binomial]] is | |
| + | : <math> (P|x) \sim \beta(\alpha+x,\beta+n-x)</math>. | ||
| + | ===Bayesian Inference for the Poisson Distribution=== | ||
| - | + | A discrete random variable x is said to have a [[EBook#Poisson_Distribution |Poisson distribution]] of mean <math>\lambda</math> if it has the density: | |
| + | : <math>P(x|\lambda) = {\lambda^x e^{-\lambda}\over x!}</math> | ||
| - | + | Suppose that you have n observations <math>x=(x_1, x_2, \cdots, x_n)</math> from such a distribution so that the likelihood is: | |
| + | : <math>L(\lambda|x) = \lambda^T e^{(-n \lambda)}</math>, where <math>T = \sum_{k_i}{x_i}</math>. | ||
| - | <math>\lambda | + | In Bayesian inference, the conjugate prior for the parameter <math>\lambda</math> of the [http://socr.ucla.edu/htmls/dist/Poisson_Distribution.html Poisson distribution] is the [http://socr.ucla.edu/htmls/dist/Gamma_Distribution.html Gamma distribution]. |
| + | : <math>\lambda \sim \Gamma(\alpha, \beta)</math>. | ||
| - | The Poisson parameter <math>\lambda</math> is distributed accordingly to the | + | The Poisson parameter <math>\lambda</math> is distributed accordingly to the parametrized Gamma density ''g'' in terms of a shape and inverse scale parameter <math>\alpha</math> and <math>\beta</math> respectively: |
| + | : <math>g(\lambda|\alpha, \beta) = \displaystyle\frac{\beta^\alpha}{\Gamma(\alpha)}\lambda^{\alpha - 1} e^{-\beta \lambda}</math>. For <math>\lambda > 0</math>. | ||
| - | + | Then, given the same sample of ''n'' measured values <math>k_i</math> from our likelihood and a prior of <math>\Gamma(\alpha, \beta)</math>, the posterior distribution becomes: | |
| - | + | : <math>\lambda \sim \Gamma (\alpha + \displaystyle\sum_{i=1}^{\infty} k_i, \beta +n)</math>. | |
| + | The posterior mean <math>E[\lambda]</math> approaches the [[EBook#Method_of_Moments_and_Maximum_Likelihood_Estimation | maximum likelihood estimate]] in the limit as <math>\alpha</math> and <math>\beta</math> approach 0. | ||
| - | + | ==See also== | |
| + | * [[EBook#Chapter_III:_Probability |Probability Chapter]] | ||
| + | ==References== | ||
| - | < | + | <hr> |
| + | * SOCR Home page: http://www.socr.ucla.edu | ||
| - | + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php?title=AP_Statistics_Curriculum_2007_Bayesian_Other}} | |
Current revision as of 20:40, 26 October 2009
Contents |
Probability and Statistics Ebook - Bayesian Inference for the Binomial and Poisson Distributions
The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a binomial distribution of index n and parameter P:
We can show that
-
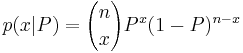 , (x = 0, 1, …, n)
, (x = 0, 1, …, n)
- p(x|P) is proportional to Px(1 − P)n − x.
If the prior density has the form:
-
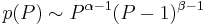 , (P between 0 and 1),
, (P between 0 and 1),
then it follows the beta distribution
-
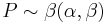 .
.
From this we can appropriate the posterior which evidently has the form:
-
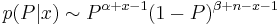 .
.
The posterior distribution of the Binomial is
-
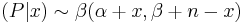 .
.
Bayesian Inference for the Poisson Distribution
A discrete random variable x is said to have a Poisson distribution of mean λ if it has the density:
Suppose that you have n observations 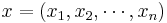 from such a distribution so that the likelihood is:
from such a distribution so that the likelihood is:
- L(λ | x) = λTe( − nλ), where
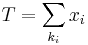 .
.
In Bayesian inference, the conjugate prior for the parameter λ of the Poisson distribution is the Gamma distribution.
-
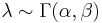 .
.
The Poisson parameter λ is distributed accordingly to the parametrized Gamma density g in terms of a shape and inverse scale parameter α and β respectively:
-
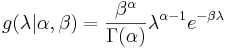 . For λ > 0.
. For λ > 0.
Then, given the same sample of n measured values ki from our likelihood and a prior of Γ(α,β), the posterior distribution becomes:
-
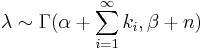 .
.
The posterior mean E[λ] approaches the maximum likelihood estimate in the limit as α and β approach 0.
See also
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: