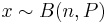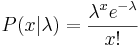AP Statistics Curriculum 2007 Bayesian Other
From Socr
m (→Probability and Statistics Ebook - Bayesian Inference for the Binomial and Poisson Distributions) |
|||
| Line 19: | Line 19: | ||
The posterior distribution of the [[EBook#Bernoulli_and_Binomial_Experiments |Binomial]] is | The posterior distribution of the [[EBook#Bernoulli_and_Binomial_Experiments |Binomial]] is | ||
| - | : <math>(P|x) \sim \beta(\alpha + x, \beta + n | + | : <math> (P|x) \sim \beta(\alpha+x,\beta+n-x)</math>. |
===Bayesian Inference for the Poisson Distribution=== | ===Bayesian Inference for the Poisson Distribution=== | ||
Current revision as of 20:40, 26 October 2009
Contents |
Probability and Statistics Ebook - Bayesian Inference for the Binomial and Poisson Distributions
The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a binomial distribution of index n and parameter P:
We can show that
-
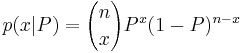 , (x = 0, 1, …, n)
, (x = 0, 1, …, n)
- p(x|P) is proportional to Px(1 − P)n − x.
If the prior density has the form:
-
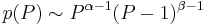 , (P between 0 and 1),
, (P between 0 and 1),
then it follows the beta distribution
-
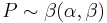 .
.
From this we can appropriate the posterior which evidently has the form:
-
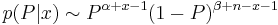 .
.
The posterior distribution of the Binomial is
-
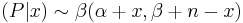 .
.
Bayesian Inference for the Poisson Distribution
A discrete random variable x is said to have a Poisson distribution of mean λ if it has the density:
Suppose that you have n observations 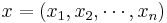 from such a distribution so that the likelihood is:
from such a distribution so that the likelihood is:
- L(λ | x) = λTe( − nλ), where
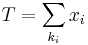 .
.
In Bayesian inference, the conjugate prior for the parameter λ of the Poisson distribution is the Gamma distribution.
-
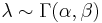 .
.
The Poisson parameter λ is distributed accordingly to the parametrized Gamma density g in terms of a shape and inverse scale parameter α and β respectively:
-
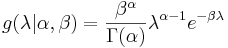 . For λ > 0.
. For λ > 0.
Then, given the same sample of n measured values ki from our likelihood and a prior of Γ(α,β), the posterior distribution becomes:
-
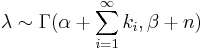 .
.
The posterior mean E[λ] approaches the maximum likelihood estimate in the limit as α and β approach 0.
See also
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: