AP Statistics Curriculum 2007 Bayesian Other
From Socr
Bayesian Inference for the Binomial Distribution
The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a binomial distribution of index n and parameter P
x ~ B(n,P)
subsequently, we can show that
p(x|P) = 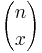 Px (1 − P)n − x , (x = 0, 1, …, n)
Px (1 − P)n − x , (x = 0, 1, …, n)
p(x|P) is proportional to Px(1 − P)n − x
If the prior density has the form: p(P) proportional to Failed to parse (lexing error): P^{α - 1} (1 – P)β – 1 , (P between 0 and 1)
then it follows the beta distribution P ~ β(α,β)
From this we can appropriate the posterior which evidently has the form
p(P|x) is proportional to Failed to parse (lexing error): P^{α + x – 1} (1 – P)^{β + n – x – 1}
The posterior distribution of the Binomial is
(P|x) ~ β(α + x, β + n – x)
