AP Statistics Curriculum 2007 Bayesian Other

From Socr

Bayesian Inference for the Binomial Distribution

The parameters of interest in this section is the probability P of success in a number of trials which can result in either success or failure with the trials being independent of one another and having the same probability of success. Suppose that there are n trials such that you have an observation of x successes from a binomial distribution of index n and parameter P

x ~ B(n,P)

subsequently, we can show that p(x|P) = 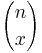P^x (1 − P)^{n − x} , (x = 0, 1, …, n)

p(x|P) is proportional to P^x(1 − P)^{n − x}

If the prior density has the form: p(P) proportional to P^{α − 1}(P − 1)^{β − 1} , (P between 0 and 1)

then it follows the beta distribution P ~ β(α,β)

From this we can appropriate the posterior which evidently has the form

p(P|x) is proportional to P^{α + x − 1}(1 − P)^{β + n − x − 1}

The posterior distribution of the Binomial is

(P|x) ~ β(α + x, β + n – x)