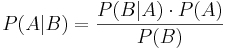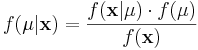AP Statistics Curriculum 2007 Bayesian Prelim
From Socr
m |
m (→Example: fixed a calculation typo (0.193 --> 0.3231293)) |
||
| (2 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
===Introduction=== | ===Introduction=== | ||
| - | Bayes | + | Bayes Theorem, or "Bayes Rule" can be stated succinctly by the equality |
: <math>P(A|B) = \frac{P(B|A) \cdot P(A)} {P(B)}</math> | : <math>P(A|B) = \frac{P(B|A) \cdot P(A)} {P(B)}</math> | ||
| Line 13: | Line 13: | ||
===Example=== | ===Example=== | ||
| - | Suppose a | + | Suppose a laboratory blood test is used as evidence for a disease. Assume P(positive Test| Disease) = 0.95, P(positive Test| no Disease)=0.01 and P(Disease) = 0.005. Find P(Disease|positive Test)=? |
Denote D = {the test person has the disease}, <math>D^c</math> = {the test person does not have the disease} and T = {the test result is positive}. Then | Denote D = {the test person has the disease}, <math>D^c</math> = {the test person does not have the disease} and T = {the test result is positive}. Then | ||
<center><math>P(D | T) = {P(T | D) P(D) \over P(T)} = {P(T | D) P(D) \over P(T|D)P(D) + P(T|D^c)P(D^c)}=</math> | <center><math>P(D | T) = {P(T | D) P(D) \over P(T)} = {P(T | D) P(D) \over P(T|D)P(D) + P(T|D^c)P(D^c)}=</math> | ||
| - | <math>={0.95\times 0.005 \over {0.95\times 0.005 +0.01\times 0.995}}=0. | + | <math>={0.95\times 0.005 \over {0.95\times 0.005 +0.01\times 0.995}}=0.3231293.</math></center> |
| - | ===Bayesian | + | ===Bayesian Statstics=== |
What is commonly called '''Bayesian Statistics''' is a very special application of Bayes Theorem. | What is commonly called '''Bayesian Statistics''' is a very special application of Bayes Theorem. | ||
| - | We will examine a number of examples in this Chapter, but to illustrate generally, imagine that '''x''' is a fixed collection of data that has been realized from | + | We will examine a number of examples in this Chapter, but to illustrate generally, imagine that '''x''' is a fixed collection of data that has been realized from some known density, <math>f(X)</math>, that takes a parameter, <math>\mu</math>, whose value is not certainly known. |
Using Bayes Theorem we may write | Using Bayes Theorem we may write | ||
Current revision as of 18:26, 20 December 2010
Contents |
Probability and Statistics Ebook - Bayes Theorem
Introduction
Bayes Theorem, or "Bayes Rule" can be stated succinctly by the equality
In words, "the probability of event A occurring given that event B occurred is equal to the probability of event B occurring given that event A occurred times the probability of event A occurring divided by the probability that event B occurs."
Bayes Theorem can also be written in terms of densities or likelihood functions over continuous random variables. Let's call  the density (or in some cases, the likelihood) defined by the random process
the density (or in some cases, the likelihood) defined by the random process  . If X and Y are random variables, we can say
. If X and Y are random variables, we can say
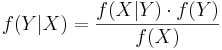
Example
Suppose a laboratory blood test is used as evidence for a disease. Assume P(positive Test| Disease) = 0.95, P(positive Test| no Disease)=0.01 and P(Disease) = 0.005. Find P(Disease|positive Test)=?
Denote D = {the test person has the disease}, Dc = {the test person does not have the disease} and T = {the test result is positive}. Then
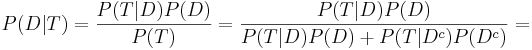
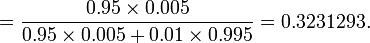
Bayesian Statstics
What is commonly called Bayesian Statistics is a very special application of Bayes Theorem.
We will examine a number of examples in this Chapter, but to illustrate generally, imagine that x is a fixed collection of data that has been realized from some known density, f(X), that takes a parameter, μ, whose value is not certainly known.
Using Bayes Theorem we may write
In this formulation, we solve for 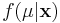 , the "posterior" density of the population parameter, μ.
, the "posterior" density of the population parameter, μ.
For this we utilize the likelihood function of our data given our parameter, 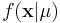 , and, importantly, a density f(μ), that describes our "prior" belief in μ.
, and, importantly, a density f(μ), that describes our "prior" belief in μ.
Since 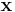 is fixed,
is fixed, 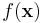 is a fixed number -- a "normalizing constant" so to ensure that the posterior density integrates to one.
is a fixed number -- a "normalizing constant" so to ensure that the posterior density integrates to one.
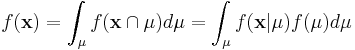
See also
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: