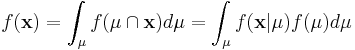AP Statistics Curriculum 2007 Bayesian Prelim
From Socr
| Line 8: | Line 8: | ||
Bayes Theorem can also be written in terms of densities over continuous random variables. So, if <math>f(\cdot)</math> is some density, and <math>X</math> and <math>Y</math> are random variables, then we can say | Bayes Theorem can also be written in terms of densities over continuous random variables. So, if <math>f(\cdot)</math> is some density, and <math>X</math> and <math>Y</math> are random variables, then we can say | ||
| - | |||
<math>f(Y|X) = \frac{f(X|Y) \cdot f(Y)} { f(X) }</math> | <math>f(Y|X) = \frac{f(X|Y) \cdot f(Y)} { f(X) }</math> | ||
| Line 26: | Line 25: | ||
Since <math>\mathbf{x}</math> is fixed, <math>f(\mathbf{x})</math>, is a fixed number -- a "normalizing constant" so to assure that the posterior density integrates to one. | Since <math>\mathbf{x}</math> is fixed, <math>f(\mathbf{x})</math>, is a fixed number -- a "normalizing constant" so to assure that the posterior density integrates to one. | ||
| - | <math>f(\mathbf{x}) = \int_{\mu} f(\mu \cap \mathbf{x}) d\mu = \int_{\mu} f( \mathbf{x} | \mu ) d\mu </math> | + | <math>f(\mathbf{x}) = \int_{\mu} f(\mu \cap \mathbf{x}) d\mu = \int_{\mu} f( \mathbf{x} | \mu ) f(\mu) d\mu </math> |
Revision as of 20:09, 23 July 2009
Bayes Theorem
Bayes theorem, or "Bayes Rule" can be stated succinctly by the equality
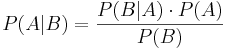
In words, "the probability of event A occurring given that event B occurred is equal to the probability of event B occurring given that event A occurred times the probability of event A occurring divided by the probability that event B occurs."
Bayes Theorem can also be written in terms of densities over continuous random variables. So, if  is some density, and X and Y are random variables, then we can say
is some density, and X and Y are random variables, then we can say
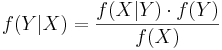
What is commonly called Bayesian Statistics is a very special application of Bayes Theorem.
We will examine a number of examples in this Chapter, but to illustrate generally, imagine that x is a fixed collection of data that has been realized from under some known density,  that takes a parameter, μ whose value is not certainly known.
that takes a parameter, μ whose value is not certainly known.
Using Bayes Theorem we may write
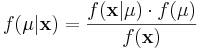
In this formulation, we solve for 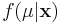 , the "posterior" density of the population parameter μ.
, the "posterior" density of the population parameter μ.
For this we utilize the likelihood function of our data given our parameter, 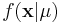 , and, importantly, a density f(μ), that describes our "prior" belief in μ.
, and, importantly, a density f(μ), that describes our "prior" belief in μ.
Since 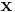 is fixed,
is fixed, 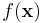 , is a fixed number -- a "normalizing constant" so to assure that the posterior density integrates to one.
, is a fixed number -- a "normalizing constant" so to assure that the posterior density integrates to one.