AP Statistics Curriculum 2007 Bayesian Prelim
From Socr
| Line 1: | Line 1: | ||
'''Bayes Theorem''' | '''Bayes Theorem''' | ||
| - | Bayes theorem can be stated succinctly by the equality | + | Bayes theorem, or "Bayes Rule" can be stated succinctly by the equality |
| - | <math>P(A|B) = P(B|A) \cdot P(A) | + | <math>P(A|B) = \frac{P(B|A) \cdot P(A)} {P(B)}</math> |
In words, "the probability of event A occurring given that event B occurred is equal to the probability of event B occurring given that event A occurred times the probability of event A occurring divided by the probability that event B occurs." | In words, "the probability of event A occurring given that event B occurred is equal to the probability of event B occurring given that event A occurred times the probability of event A occurring divided by the probability that event B occurs." | ||
| Line 9: | Line 9: | ||
Bayes Theorem can also be written in terms of densities over continuous random variables. So, if <math>f(\cdot)</math> is some density, and <math>X</math> and <math>Y</math> are random variables, then we can say | Bayes Theorem can also be written in terms of densities over continuous random variables. So, if <math>f(\cdot)</math> is some density, and <math>X</math> and <math>Y</math> are random variables, then we can say | ||
| - | |||
<math>f(Y|X) = \frac{f(X|Y) \cdot f(Y)} { f(X) }</math> | <math>f(Y|X) = \frac{f(X|Y) \cdot f(Y)} { f(X) }</math> | ||
| + | |||
| + | What is commonly called '''Bayesian Statistics''' is a very special application of Bayes Theorem. | ||
| + | |||
| + | We will examine a number of examples in this Chapter, but to illustrate generally, imagine that '''x''' is a fixed collection of data that has been realized from under some density, <math>f(\cdot)</math> that takes a parameter, <math>\mu</math> whose value is not certainly known. | ||
| + | |||
| + | Using Bayes Theorem we may write | ||
| + | |||
| + | <math>f(\mu|\mathbf{x}) = \frac{f(\mathbf{x}|\mu) \cdot f(\mu)} { f(\mathbf) }</math> | ||
Revision as of 18:59, 23 July 2009
Bayes Theorem
Bayes theorem, or "Bayes Rule" can be stated succinctly by the equality
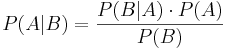
In words, "the probability of event A occurring given that event B occurred is equal to the probability of event B occurring given that event A occurred times the probability of event A occurring divided by the probability that event B occurs."
Bayes Theorem can also be written in terms of densities over continuous random variables. So, if  is some density, and X and Y are random variables, then we can say
is some density, and X and Y are random variables, then we can say
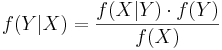
What is commonly called Bayesian Statistics is a very special application of Bayes Theorem.
We will examine a number of examples in this Chapter, but to illustrate generally, imagine that x is a fixed collection of data that has been realized from under some density,  that takes a parameter, μ whose value is not certainly known.
that takes a parameter, μ whose value is not certainly known.
Using Bayes Theorem we may write
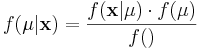
is associated with probability statements that relate conditional and marginal properties of two random events. These statements are often written in the form "the probability of A, given B" and denoted P(A|B) = P(B|A)*P(A)/P(B) where P(B) not equal to 0.
P(A) is often known as the Prior Probability (or as the Marginal Probability)
P(A|B) is known as the Posterior Probability (Conditional Probability)
P(B|A) is the conditional probability of B given A (also known as the likelihood function)
P(B) is the prior on B and acts as the normalizing constant. In the Bayesian framework, the posterior probability is equal to the prior belief on A times the likelihood function given by P(B|A).
