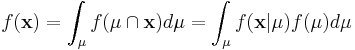AP Statistics Curriculum 2007 Bayesian Prelim
From Socr
Bayes Theorem
Bayes theorem, or "Bayes Rule" can be stated succinctly by the equality
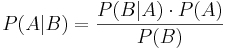
In words, "the probability of event A occurring given that event B occurred is equal to the probability of event B occurring given that event A occurred times the probability of event A occurring divided by the probability that event B occurs."
Bayes Theorem can also be written in terms of densities over continuous random variables. So, if  is some density, and X and Y are random variables, then we can say
is some density, and X and Y are random variables, then we can say
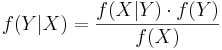
What is commonly called Bayesian Statistics is a very special application of Bayes Theorem.
We will examine a number of examples in this Chapter, but to illustrate generally, imagine that x is a fixed collection of data that has been realized from under some known density,  , that takes a parameter, μ, whose value is not certainly known.
, that takes a parameter, μ, whose value is not certainly known.
Using Bayes Theorem we may write
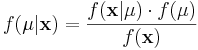
In this formulation, we solve for 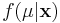 , the "posterior" density of the population parameter, μ.
, the "posterior" density of the population parameter, μ.
For this we utilize the likelihood function of our data given our parameter, 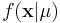 , and, importantly, a density f(μ), that describes our "prior" belief in μ.
, and, importantly, a density f(μ), that describes our "prior" belief in μ.
Since 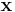 is fixed,
is fixed, 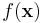 is a fixed number -- a "normalizing constant" so to ensure that the posterior density integrates to one.
is a fixed number -- a "normalizing constant" so to ensure that the posterior density integrates to one.