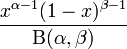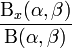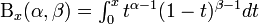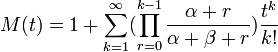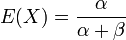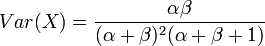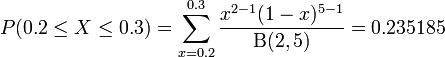AP Statistics Curriculum 2007 Beta
From Socr
(→Beta Distribution) |
|||
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| + | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Beta Distribution== | ||
| + | |||
===Beta Distribution=== | ===Beta Distribution=== | ||
'''Definition''': Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value. | '''Definition''': Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value. | ||
| Line 46: | Line 48: | ||
The figure below shows this result using [http://socr.ucla.edu/htmls/dist/Beta_Distribution.html SOCR distributions] | The figure below shows this result using [http://socr.ucla.edu/htmls/dist/Beta_Distribution.html SOCR distributions] | ||
<center>[[Image:Beta.jpg|600px]]</center> | <center>[[Image:Beta.jpg|600px]]</center> | ||
| + | |||
| + | <hr> | ||
| + | * SOCR Home page: http://www.socr.ucla.edu | ||
| + | |||
| + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php/AP_Statistics_Curriculum_2007_Beta}} | ||
Current revision as of 22:35, 18 July 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Beta Distribution
Beta Distribution
Definition: Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value.
Probability density function: For  , the Beta probability density function is given by
, the Beta probability density function is given by
where
- α is a positive shape parameter
- β is a positive shape parameter
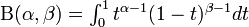 or
or 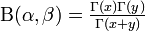 , where
, where 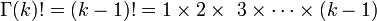
- x is a random variable
Cumulative density function: Beta cumulative distribution function is given by
where
Moment generating function: The Beta moment-generating function is
Expectation: The expected value of a Beta distributed random variable x is
Variance: The Beta variance is
Applications
The Beta distribution is used in a range of disciplines including rule of succession, Bayesian statistics, and task duration modeling. Examples of events that may be modeled by Beta distribution include:
- The time it takes to complete a task
- The proportion of defective items in a shipment
Example
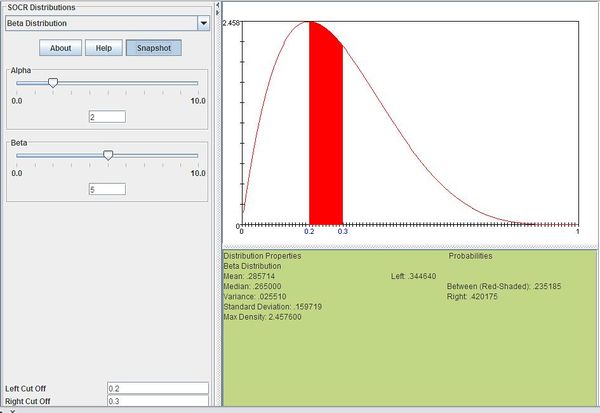
Suppose that DVDs in a certain shipment are defective with a Beta distribution with α = 2 and β = 5. Compute the probability that the shipment has 20% to 30% defective DVDs.
We can compute this as follows:
The figure below shows this result using SOCR distributions
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: