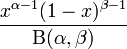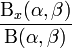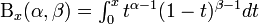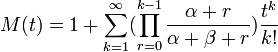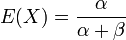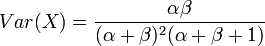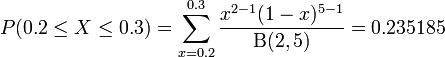AP Statistics Curriculum 2007 Beta
From Socr
(→Beta Distribution) |
(→Beta Distribution) |
||
| Line 18: | Line 18: | ||
where | where | ||
| - | *<math>\Beta_x(\alpha,\beta)=\int_0^x t^{\alpha-1}(1-t)^{\beta-1}dt</math> | + | *<math>\textstyle\Beta_x(\alpha,\beta)=\int_0^x t^{\alpha-1}(1-t)^{\beta-1}dt</math> |
| - | *<math>\Beta(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt</math> | + | *<math>\textstyle\Beta(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt</math> |
<br />'''Moment generating function''': The Beta moment-generating function is | <br />'''Moment generating function''': The Beta moment-generating function is | ||
Revision as of 20:55, 11 July 2011
Beta Distribution
Definition: Beta distribution is a distribution that models events which are constrained to take place within an interval defined by a minimum and maximum value.
Probability density function: For 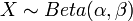 , the Beta probability density function is given by
, the Beta probability density function is given by
where
- α is a positive shape parameter
- β is a positive shape parameter
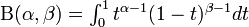 or
or
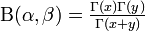 , where
, where 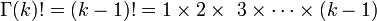
- x is a random variable
Cumulative density function: Beta cumulative distribution function is given by
where
Moment generating function: The Beta moment-generating function is
Expectation: The expected value of a Beta distributed random variable x is
Variance: The Beta variance is
Applications
The Beta distribution is used in a range of disciplines including rule of succession, Bayesian statistics, and task duration modeling. Examples of events that may be modeled by Beta distribution include:
- The time it takes to complete a task
- The proportion of defective items in a shipment
Example
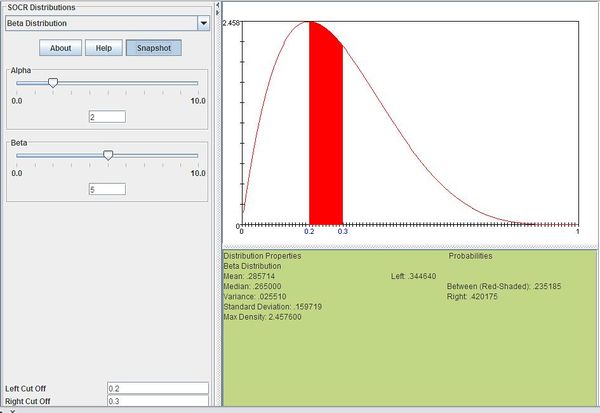
Suppose that DVDs in a certain shipment are defective with a Beta distribution with α=2 and β=5. Compute the probability that the shipment has 20% to 30% defective DVDs.
We can compute this as follows:
The figure below shows this result using SOCR distributions