AP Statistics Curriculum 2007 Cauchy
From Socr
(Created page with '== General Advance-Placement (AP) Statistics Curriculum - Cauchy Distribution== === Cauchy Distribution === The standard Cauchy distribution i…') |
|||
| Line 55: | Line 55: | ||
* SOCR Home page: http://www.socr.ucla.edu | * SOCR Home page: http://www.socr.ucla.edu | ||
| - | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php | + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php/AP_Statistics_Curriculum_2007_Cauchy}} |
Revision as of 21:58, 30 June 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Cauchy Distribution
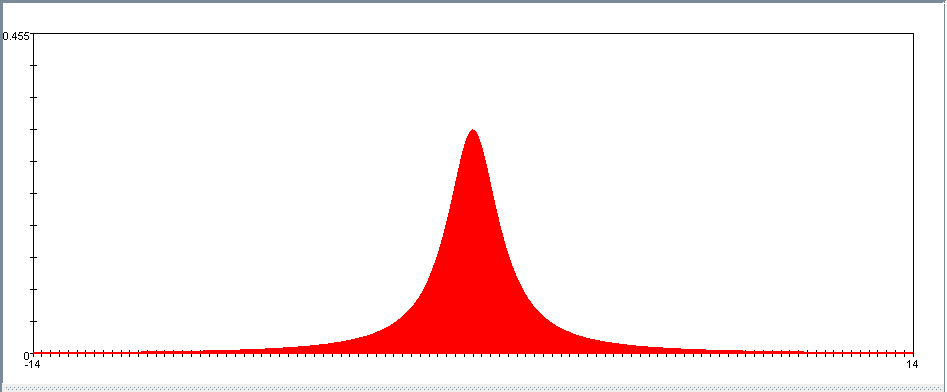
Cauchy Distribution
The standard Cauchy distribution is derived from the ratio of two independent Normal distributions. If X ~ N(0,1), and Y ~ N(0,1), then 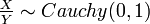
The Cauchy distribution is important in physics (where it’s known as the Lorentz distribution) because it’s the solution to the differential equation describing forced resonance. In spectroscopy, it is the description of the shape of spectral lines which are subject to homogeneous broadening in which all atoms interact in the same way with the frequency range contained in the line shape.
PDF:
![\frac{1}{\pi\gamma\,\left[1 + \left(\frac{x-x_0}{\gamma}\right)^2\right]}\!](/socr/uploads/math/1/1/0/110abf1f3bbdd637b6ddd41296caa067.png)
CDF:

Mean:
Does Not Exist
Median:

Variance:
Does Not Exist
Support:
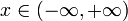
1st Moment:
None
2nd Moment:
None
Kth Moment:
None
Applications
 Used in mechanical and electrical theory, physical anthropology and measurement and calibration problems.
Used in mechanical and electrical theory, physical anthropology and measurement and calibration problems.
 In physics it is called a Lorentzian distribution, where it is the distribution of the energy of an unstable state in quantum mechanics.
In physics it is called a Lorentzian distribution, where it is the distribution of the energy of an unstable state in quantum mechanics.
 Also used to model the points of impact of a fixed straight line of particles emitted from a point source.
Also used to model the points of impact of a fixed straight line of particles emitted from a point source.
Example
SOCR Links
http://www.distributome.org/ -> SOCR -> Distributions -> Distributome
http://www.distributome.org/ -> SOCR -> Distributions -> Cauchy Distribution
http://www.distributome.org/ -> SOCR -> Functors -> Cauchy Distribution
SOCR Cauchy Distribution calculator (http://socr.ucla.edu/htmls/dist/Cauchy_Distribution.html)
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: