AP Statistics Curriculum 2007 Chi-Square
From Socr
| Line 25: | Line 25: | ||
''x'' ∈ [0, +∞) | ''x'' ∈ [0, +∞) | ||
| - | ''' | + | ====Raw Moments==== |
| - | k | + | The ''k''<sup>th</sup> '''Raw Moment''' for a discrete random variable ''X'' is defined by <math>E[X^k]=\sum_x{x^kP(X=x)}.</math> The ''k''<sup>th</sup> '''Raw Moment''' for a continuously-values random variable ''Y'' is analogously defined by <math>E[Y^k]=\int{y^kP(y)dy},</math> where the integral is over the domain of ''Y'' and ''P(y)'' is the probability density function of ''Y''. |
| - | ''' | + | ====Centralized Moments==== |
| - | + | The ''k''<sup>th</sup> '''Centralized Moment''' for a discrete random variable ''X'' is defined by <math>E_c[X^k]=\sum_x{(x-\mu)^kP(X=x)},</math> where <math>\mu</math> is the expected value of ''X''. The ''k''<sup>th</sup> '''Centralized Moment''' for a continuously-values random variable ''Y'' is analogously defined by <math>E_c[Y^k]=\int{(y-\mu)^kP(y)dy},</math> where <math>\mu</math> is the expected value of ''Y'', the integral is over the domain of ''Y'' and ''P(y)'' is the probability density function of ''Y''. | |
| + | ====Standardized Moments==== | ||
| + | The ''k''<sup>th</sup> '''Standardized Moment''' for a discrete random variable ''X'' is defined by | ||
| + | |||
| + | : <math>E_s[X^k]={\sum_x{(x-\mu)^kP(X=x)} \over {(\sum_{x} (x-\mu)^2P(X=x))^{k/2}}}.</math> | ||
| + | |||
| + | The ''k''<sup>th</sup> '''Standardized Moment''' for a continuously-values random variable ''Y'' is analogously defined by | ||
| + | |||
| + | :<math>E_s[Y^k]={\int{(y-\mu)^kP(y)dy} \over \sigma^k},</math> where the integral is over the domain of ''Y'' and ''P(y)'' is the probability density function of ''Y'' | ||
===Applications=== | ===Applications=== | ||
<math>\cdot</math> [http://en.wikipedia.org/wiki/Goodness_of_fit Chi-Square goodness of fit] | <math>\cdot</math> [http://en.wikipedia.org/wiki/Goodness_of_fit Chi-Square goodness of fit] | ||
Revision as of 21:32, 2 July 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Chi-Square Distribution
Chi-Square Distribution
The Chi-Square distribution is used in the chi-square tests for goodness of fit of an observed distribution to a theoretical one and the independence of two criteria of classification of qualitative data. It is also used in confidence interval estimation for a population standard deviation of a normal distribution from a sample standard deviation. The Chi-Square distribution is a special case of the Gamma distribution [link to gamma].
PDF:
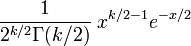
CDF:

Mean:
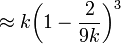
Median:
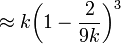
Mode:
max{ k − 2, 0 }
Variance:
2k
Support:
x ∈ [0, +∞)
Raw Moments
The kth Raw Moment for a discrete random variable X is defined by| E[Xk] = | ∑ | xkP(X = x). |
| x |
![E[Y^k]=\int{y^kP(y)dy},](/socr/uploads/math/1/b/0/1b0276799e29d88e58517f36b4ee7506.png) where the integral is over the domain of Y and P(y) is the probability density function of Y.
where the integral is over the domain of Y and P(y) is the probability density function of Y.
Centralized Moments
The kth Centralized Moment for a discrete random variable X is defined by| Ec[Xk] = | ∑ | (x − μ)kP(X = x), |
| x |
![E_c[Y^k]=\int{(y-\mu)^kP(y)dy},](/socr/uploads/math/0/0/7/00707fca33eb89717efcd84364a75654.png) where μ is the expected value of Y, the integral is over the domain of Y and P(y) is the probability density function of Y.
where μ is the expected value of Y, the integral is over the domain of Y and P(y) is the probability density function of Y.
Standardized Moments
The kth Standardized Moment for a discrete random variable X is defined by
The kth Standardized Moment for a continuously-values random variable Y is analogously defined by
![E_s[Y^k]={\int{(y-\mu)^kP(y)dy} \over \sigma^k},](/socr/uploads/math/d/f/d/dfd27aef870d59af11c6b2ed852867a0.png) where the integral is over the domain of Y and P(y) is the probability density function of Y
where the integral is over the domain of Y and P(y) is the probability density function of Y
Applications
 Independence of two criteria of classification of qualitative data
Independence of two criteria of classification of qualitative data
 Confidence Interval estimation for a population standard deviation of a normal distribution from a sample standard deviation
Confidence Interval estimation for a population standard deviation of a normal distribution from a sample standard deviation
 ANOVA: The F distribution is distribution of two independent chi-square random variables, divided by their respective degrees of freedom [link to Fisher’s F, ANOVA]
ANOVA: The F distribution is distribution of two independent chi-square random variables, divided by their respective degrees of freedom [link to Fisher’s F, ANOVA]
Example
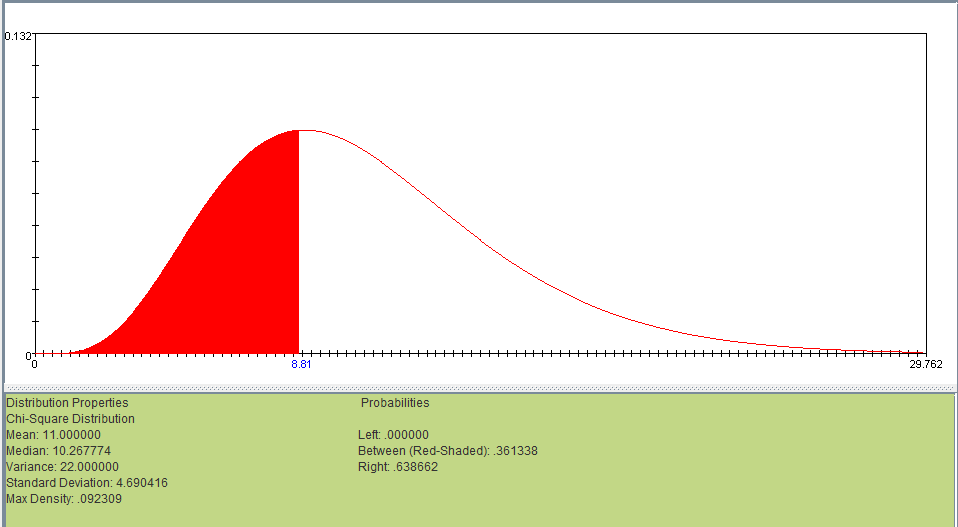
Chi Square Test for Goodness of Fit: There are 60 people in a statistics class, and we have data on the month of their birth. Our null hypothesis is that the number of students with a particular birth month should be divided equally among the total 60. We can use a chi square test with 12-1=11 degrees of freedom to compare the observed data against our null hypothesis.
| Birthday Month | Observed | Expected | Residual (Obs-Exp) | (Obs − Exp)2 | (Obs − Exp)2 / Exp |
|---|---|---|---|---|---|
| Jan | 3 | 5 | -2 | 4 | 0.8 |
| Feb | 4 | 5 | -1 | 1 | 0.2 |
| Mar | 8 | 5 | 3 | 9 | 1.8 |
| April | 4 | 5 | -1 | 1 | 0.2 |
| May | 2 | 5 | -3 | 9 | 1.8 |
| June | 3 | 5 | -2 | 4 | 0.8 |
| July | 6 | 5 | 1 | 1 | 0.2 |
| Aug | 6 | 5 | 1 | 1 | 0.2 |
| Sept | 4 | 5 | -1 | 1 | 0.2 |
| Oct | 3 | 5 | -2 | 4 | 0.8 |
| Nov | 2 | 5 | -3 | 9 | 1.8 |
| Dec | 5 | 5 | 0 | 0 | 0 |
| Total = | 8.8 |
Our Chi Square value is 8.8. Using the SOCR Chi-Square Distribution Calculator, at 11 degrees of freedom, a chi square value of 8.8 gives us a p-value of 0.36. We do not reject our null hypothesis. The observed data do not show evidence of a non-uniform distribution of birth months.
SOCR Links
http://www.distributome.org/ -> SOCR -> Distributions -> Distributome
http://www.distributome.org/ -> SOCR -> Distributions -> Chi-Square Distribution
http://www.distributome.org/ -> SOCR -> Functors -> Chi-Square Distribution
http://www.distributome.org/ -> SOCR -> Analyses -> Chi-Square Test Contingency Table
http://www.distributome.org/ -> SOCR -> Analyses -> Chi-Square Model Goodness-of-Fit Test
http://www.distributome.org/ -> SOCR -> Modeler -> ChiSquareFit_Modeler
SOCR Chi-Square Distribution Calculator (http://socr.ucla.edu/htmls/dist/ChiSquare_Distribution.html)
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
![E_s[X^k]={\sum_x{(x-\mu)^kP(X=x)} \over {(\sum_{x} (x-\mu)^2P(X=x))^{k/2}}}.](/socr/uploads/math/3/d/6/3d62db48d2060b237b49a1ea59dc43a1.png)