AP Statistics Curriculum 2007 Contingency Fit
From Socr
(→Calculations) |
|||
| Line 21: | Line 21: | ||
==Calculations== | ==Calculations== | ||
| - | Suppose there were ''N = 1064'' data measurements with ''Observed(Tall) = 787'' and ''Observed(Dwarf) = 277''. These are the O’s (observed values). To calculate the E’s (expected values), we will take the hypothesized proportions under <math>H_o</math> and multiply them by the total sample size ''N''. Expected(Tall) = (0.75)(1064) = 798 and Expected(Dwarf) = (0.25)(1064) = 266 | + | Suppose there were ''N = 1064'' data measurements with ''Observed(Tall) = 787'' and ''Observed(Dwarf) = 277''. These are the O’s (observed values). To calculate the E’s (expected values), we will take the hypothesized proportions under <math>H_o</math> and multiply them by the total sample size ''N''. Expected(Tall) = (0.75)(1064) = 798 and Expected(Dwarf) = (0.25)(1064) = 266. Quickly check to see if the expected total = N = 1064. |
| - | Quickly check to see if the expected total = N = 1064. | + | |
* The hypotheses: | * The hypotheses: | ||
| Line 29: | Line 28: | ||
: <math>H_a</math>: P(tall) ≠ 0.75 | : <math>H_a</math>: P(tall) ≠ 0.75 | ||
::P(dwarf) ≠ 0.25 | ::P(dwarf) ≠ 0.25 | ||
| + | |||
| + | * Test statistics: | ||
| + | :<math>\chi_o^2 = \sum_{all-categories}{(O-E)^2/E} \sim \chi_{df=number\_of\_categories - 1}^2</math> | ||
| + | |||
| + | * P-values and critical values for the [http://socr.stat.ucla.edu/htmls/SOCR_Distributions.html Chi-Square distribution may be easily computed using SOCR Distributions]. | ||
| + | |||
| + | * Results: | ||
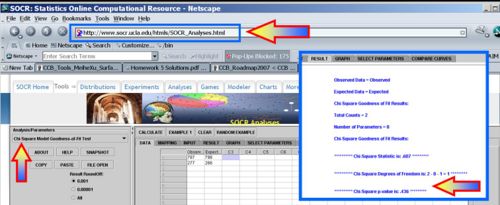
| + | For the Mendel's pea experiment, we can compute the Chi-square test statistics to be: | ||
| + | : <math>\chi_o^2 = {(787-798)^2 \over 798} + {(277-266)@ \over 266} = 0.152+0.455=0.607</math>. | ||
| + | : p-value=<math>P(Chi^2 > \chi_o^2)=0.436</math> | ||
| + | |||
| + | * SOCR Chi-square Caluclations | ||
| + | |||
| + | <center>[[Image:SOCR_EBook_Dinov_ChiSquare_030108_Fig1.jpg|500px]]</center> | ||
Revision as of 02:10, 3 March 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Multinomial Experiments: Chi-Square Goodness-of-Fit
The chi-square test is used to test if a data sample comes from a population with a specific characteristics. The chi-square goodness-of-fit test is applied to binned data (data put into classes or categoris). In most situations, the data histogram or frequency histogram may be obtained and the chi-square test may be applied to these (frequency) values. The chi-square test requires a sufficient sample size in order for the chi-square approximation to be valid.
The Kolmogorov-Smirnov is an alternative to the Chi-square goodness-of-fit test. The chi-square goodness-of-fit test may also be applied to discrete distributions such as the binomial and the Poisson. The Kolmogorov-Smirnov test is restricted to continuous distributions.
Motivational example
Mendel's pea experiment relates to the transmission of hereditary characteristics from parent organisms to their offspring; it underlies much of genetics. Suppose a tall offspring is the event of interest and that the true proportion of tall peas (based on a 3:1 phenotypic ratio) is 3/4 or p = 0.75. He would like to show that Mendel's data follow this 3:1 phenotypic ratio.
| Observed (O) | Expected (E) | |
| Tall | 787 | 798 |
| Dwarf | 277 | 266 |
Calculations
Suppose there were N = 1064 data measurements with Observed(Tall) = 787 and Observed(Dwarf) = 277. These are the O’s (observed values). To calculate the E’s (expected values), we will take the hypothesized proportions under Ho and multiply them by the total sample size N. Expected(Tall) = (0.75)(1064) = 798 and Expected(Dwarf) = (0.25)(1064) = 266. Quickly check to see if the expected total = N = 1064.
- The hypotheses:
- Ho:P(tall) = 0.75 (No effect, follows a 3:1phenotypic ratio)
- P(dwarf) = 0.25
- Ha: P(tall) ≠ 0.75
- P(dwarf) ≠ 0.25
- Test statistics:
- P-values and critical values for the Chi-Square distribution may be easily computed using SOCR Distributions.
- Results:
For the Mendel's pea experiment, we can compute the Chi-square test statistics to be:
- Failed to parse (lexing error): \chi_o^2 = {(787-798)^2 \over 798} + {(277-266)@ \over 266} = 0.152+0.455=0.607
.
- p-value=
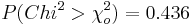
- SOCR Chi-square Caluclations
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:

