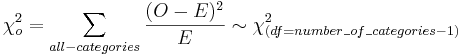AP Statistics Curriculum 2007 Contingency Fit
From Socr
(→Calculations) |
|||
| Line 43: | Line 43: | ||
<center>[[Image:SOCR_EBook_Dinov_ChiSquare_030108_Fig1.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_ChiSquare_030108_Fig1.jpg|500px]]</center> | ||
| + | ==Examples== | ||
| + | |||
| + | ===Butterfly Hotspots=== | ||
| + | A hotspot is defined as a <math>10 km^2</math> area that is species rich (heavily populated by the species of interest). Suppose in a study of butterfly hotspots in a particular region, the number of butterfly hotspots in a sample of 2,588, <math>10 km^2</math> areas is 165. In theory, 5% of the areas should be butterfly hotspots. Do the data provide evidence to suggest that the number of butterfly hotspots is increasing from the theoretical standards? Test using <math>\alpha= 0.01</math>. | ||
| + | |||
| + | ===Cell-Phone Usage=== | ||
| + | Of 250 randomly selected cell phone users, is there evidence to show that there is a difference in area of home residence, defined as: Northern California (North); Southern California (South); or Out of State (Out)? Without further information suppose we have P(North) = 0.24, P(South) = 0.45, and P(Out) = 0.31. Is there any evidence suggesting different use of cell phones in these three groups of users? | ||
| + | |||
| + | ===Brain Cancer=== | ||
| + | Suppose 200 randomly selected cancer patients were asked if their primary diagnosis was Brain cancer and if they owned a cell phone before their diagnosis. The results are presented in the table below: | ||
| + | |||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:25%" border="1" | ||
| + | |- | ||
| + | | colspan=5| '''Brain cancer''' | ||
| + | |- | ||
| + | | || || Yes || No || Total | ||
| + | |- | ||
| + | | rowspan=3| '''Cell Phone Use''' || Yes || 18 || 80 || 98 | ||
| + | |- | ||
| + | | No || 7 || 95 || 102 | ||
| + | |- | ||
| + | | Total || 25 || 175 || 200 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | Does it seem like there is an association between brain cancer and cell phone use? | ||
| + | Of the brain cancer patients 18/25 = 0.72, owned a cell phone before their diagnosis. | ||
| + | ''P(CP|BC) = 0.72'', estimated probability of owning a cell phone given that the patient has brain cancer. | ||
| + | |||
| + | Of the other cancer patients, 80/175 = 0.46, owned a cell phone before their diagnosis. | ||
| + | ''P(CP|NBC) = 0.46'', estimated probability of owning a cell phone given that the patient has another cancer. | ||
| + | |||
| + | ==Applications== | ||
| + | |||
| + | ===Polynomial Model Fitting=== | ||
| + | [http://socr.stat.ucla.edu/Applets.dir/SOCRCurveFitter.html This applet demonstrated the use of the Chi-Square test to assess quality of fitting a polynomial model (of any degree) to manually drawn curves]. | ||
<hr> | <hr> | ||
Revision as of 02:26, 3 March 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Multinomial Experiments: Chi-Square Goodness-of-Fit
The chi-square test is used to test if a data sample comes from a population with a specific characteristics. The chi-square goodness-of-fit test is applied to binned data (data put into classes or categoris). In most situations, the data histogram or frequency histogram may be obtained and the chi-square test may be applied to these (frequency) values. The chi-square test requires a sufficient sample size in order for the chi-square approximation to be valid.
The Kolmogorov-Smirnov is an alternative to the Chi-square goodness-of-fit test. The chi-square goodness-of-fit test may also be applied to discrete distributions such as the binomial and the Poisson. The Kolmogorov-Smirnov test is restricted to continuous distributions.
Motivational example
Mendel's pea experiment relates to the transmission of hereditary characteristics from parent organisms to their offspring; it underlies much of genetics. Suppose a tall offspring is the event of interest and that the true proportion of tall peas (based on a 3:1 phenotypic ratio) is 3/4 or p = 0.75. He would like to show that Mendel's data follow this 3:1 phenotypic ratio.
| Observed (O) | Expected (E) | |
| Tall | 787 | 798 |
| Dwarf | 277 | 266 |
Calculations
Suppose there were N = 1064 data measurements with Observed(Tall) = 787 and Observed(Dwarf) = 277. These are the O’s (observed values). To calculate the E’s (expected values), we will take the hypothesized proportions under Ho and multiply them by the total sample size N. Expected(Tall) = (0.75)(1064) = 798 and Expected(Dwarf) = (0.25)(1064) = 266. Quickly check to see if the expected total = N = 1064.
- The hypotheses:
- Ho:P(tall) = 0.75 (No effect, follows a 3:1phenotypic ratio)
- P(dwarf) = 0.25
- Ha: P(tall) ≠ 0.75
- P(dwarf) ≠ 0.25
- Test statistics:
- P-values and critical values for the Chi-Square distribution may be easily computed using SOCR Distributions.
- Results:
For the Mendel's pea experiment, we can compute the Chi-square test statistics to be:
-
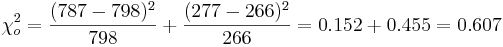 .
.
- p-value=
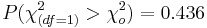
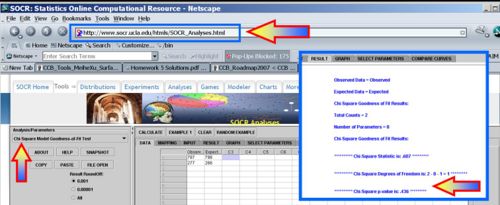
- SOCR Chi-square Caluclations
Examples
Butterfly Hotspots
A hotspot is defined as a 10km2 area that is species rich (heavily populated by the species of interest). Suppose in a study of butterfly hotspots in a particular region, the number of butterfly hotspots in a sample of 2,588, 10km2 areas is 165. In theory, 5% of the areas should be butterfly hotspots. Do the data provide evidence to suggest that the number of butterfly hotspots is increasing from the theoretical standards? Test using α = 0.01.
Cell-Phone Usage
Of 250 randomly selected cell phone users, is there evidence to show that there is a difference in area of home residence, defined as: Northern California (North); Southern California (South); or Out of State (Out)? Without further information suppose we have P(North) = 0.24, P(South) = 0.45, and P(Out) = 0.31. Is there any evidence suggesting different use of cell phones in these three groups of users?
Brain Cancer
Suppose 200 randomly selected cancer patients were asked if their primary diagnosis was Brain cancer and if they owned a cell phone before their diagnosis. The results are presented in the table below:
| Brain cancer | ||||
| Yes | No | Total | ||
| Cell Phone Use | Yes | 18 | 80 | 98 |
| No | 7 | 95 | 102 | |
| Total | 25 | 175 | 200 | |
Does it seem like there is an association between brain cancer and cell phone use? Of the brain cancer patients 18/25 = 0.72, owned a cell phone before their diagnosis. P(CP|BC) = 0.72, estimated probability of owning a cell phone given that the patient has brain cancer.
Of the other cancer patients, 80/175 = 0.46, owned a cell phone before their diagnosis. P(CP|NBC) = 0.46, estimated probability of owning a cell phone given that the patient has another cancer.
Applications
Polynomial Model Fitting
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: