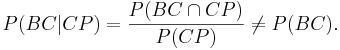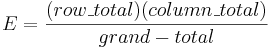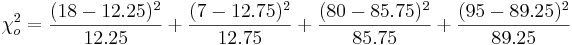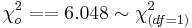AP Statistics Curriculum 2007 Contingency Indep
From Socr
(added a link to the Problems set) |
|||
| (4 intermediate revisions not shown) | |||
| Line 17: | Line 17: | ||
{| class="wikitable" style="text-align:center; width:25%" border="1" | {| class="wikitable" style="text-align:center; width:25%" border="1" | ||
|- | |- | ||
| - | | | + | | colspan=2 rowspan=2| || colspan=3| '''Brain cancer''' |
|- | |- | ||
| - | + | | '''Yes''' || '''No''' || '''Total''' | |
|- | |- | ||
| rowspan=3| '''Cell Phone Use''' || '''Yes''' || 18 || 80 || 98 | | rowspan=3| '''Cell Phone Use''' || '''Yes''' || 18 || 80 || 98 | ||
| Line 39: | Line 39: | ||
* The Hypotheses: | * The Hypotheses: | ||
| - | : <math>H_o</math>: | + | : <math>H_o</math>: There is no association between variable 1 and variable 2 (independence) |
:: ''P(BC|CP)=P(BC)'', that is brain-cancer (BC) is independent of cell-phone (CP) usage. | :: ''P(BC|CP)=P(BC)'', that is brain-cancer (BC) is independent of cell-phone (CP) usage. | ||
| - | : <math>H_a</math>: | + | : <math>H_a</math>: There is an association between variable 1 and variable 2 (dependence) |
:: <math>P(BC|CP)={P(BC \cap CP) \over P(CP) } \not= P(BC).</math> | :: <math>P(BC|CP)={P(BC \cap CP) \over P(CP) } \not= P(BC).</math> | ||
| Line 75: | Line 75: | ||
===Earthquake Insurance Example=== | ===Earthquake Insurance Example=== | ||
| - | Many factors are considered when purchasing earthquake insurance. One factor of interest may be location with respect to a major earthquake fault. Suppose a survey | + | Many factors are considered when purchasing earthquake insurance. One factor of interest may be location with respect to a major earthquake fault. Suppose a survey is mailed to California residents in four counties (data shown below). Is there a statistically significant association between county of residence and purchase of earthquake insurance? Test using a = 0.05. |
<center> | <center> | ||
{| class="wikitable" style="text-align:center; width:25%" border="1" | {| class="wikitable" style="text-align:center; width:25%" border="1" | ||
|- | |- | ||
| - | | | + | | colspan=2 rowspan=2 | || colspan=5| '''County''' |
|- | |- | ||
| - | + | | '''Contra Costa''' (CC) || '''Santa Clara''' (SC) || '''Los Angeles''' (LA) || '''San Bernardino''' (SB) || '''Total''' | |
|- | |- | ||
| rowspan=3| '''Earthquake Insurance''' || '''Yes''' || 117 || 222 || 133 || 109 || 581 | | rowspan=3| '''Earthquake Insurance''' || '''Yes''' || 117 || 222 || 133 || 109 || 581 | ||
| Line 105: | Line 105: | ||
===Moths Memory from Caterpillar Stage=== | ===Moths Memory from Caterpillar Stage=== | ||
| - | [[AP_Statistics_Curriculum_2007_Contingency_Indep#References | One study (Blackiston, Casey and Weiss, 2008)]] showed that moths can remember something they learned at caterpillar stage -- an association of an odor with an electric shock. This memory remains even though the metamorphosis | + | [[AP_Statistics_Curriculum_2007_Contingency_Indep#References | One study (Blackiston, Casey and Weiss, 2008)]] showed that moths can remember something they learned at caterpillar stage -- an association of an odor with an electric shock. This memory remains even though the metamorphosis decomposes much of their entire (caterpillar) body and reconstitutes it again (as a moth). |
| - | [http://en.wikipedia.org/wiki/Manduca_sexta Tobacco hornworm moth caterpillars] were put into one of 4 treatment groups: ''control'', ''shock'', ''odor'', or ''shock and odor''. Then the moths were observed to see whether they avoided the ''odor''. If the moths could "remember" the odor association with shock, then one would expect a greater rate of avoidance of odor in the moths in the last group. The empirical results seem to provide evidence in | + | [http://en.wikipedia.org/wiki/Manduca_sexta Tobacco hornworm moth caterpillars] were put into one of 4 treatment groups: ''control'', ''shock'', ''odor'', or ''shock and odor''. Then the moths were observed to see whether they avoided the ''odor''. If the moths could "remember" the odor association with shock, then one would expect a greater rate of avoidance of odor in the moths in the last group. The empirical results seem to provide evidence in supporting this hypothesis. This study employed a classical conditioning to train caterpillars to avoid the ''odor of ethyl acetate (EA)'' by pairing odor with a mild electric shock. The data are included in the table below. |
<center> | <center> | ||
| Line 124: | Line 124: | ||
</center> | </center> | ||
| - | Use the SOCR Chi-square test of association to find out if indeed the data | + | Use the SOCR Chi-square test of association to find out if indeed the data support a research hypothesis that training memory may proliferate through the transition process of metamorphosis from caterpillar to moth. Also establish that the first three groups don't deviate significantly from the (null hypothesis) 50% avoidance level. Therefore, the moths seem naturally unaffected by the odor itself. You can also show that the '''Shock + Odor''' treatment group has an avoidance of the odor rate significantly higher than 0.5 (given by the null hypothesis). |
<center>[[Image:SOCR_EBook_Dinov_ChiSquare_030308_Fig4.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_ChiSquare_030308_Fig4.jpg|500px]]</center> | ||
| Line 136: | Line 136: | ||
: ''P-value = 0.029529758678132345'' indicates that there is an association between these two variables. | : ''P-value = 0.029529758678132345'' indicates that there is an association between these two variables. | ||
| - | We can also test to see if within each treatment group, there is a strong group separation between the moths that ''avoided the EA odor'' and those that ''did not''. Recall that this | + | We can also test to see if within each treatment group, there is a strong group separation between the moths that ''avoided the EA odor'' and those that ''did not''. Recall that this can be done by the [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair |sign-test]]. |
| - | : '''Controls''': <math>x_o =25</math>, and <math>P(x_o > 25) =0.230696</math>, when <math>x_o \sim Binomial(N = 46, p = 0.5)</math>. Thus, we | + | : '''Controls''': <math>x_o =25</math>, and <math>P(x_o > 25) =0.230696</math>, when <math>x_o \sim Binomial(N = 46, p = 0.5)</math>. Thus, we cannot reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid the odor are different (within the '''Control group'''). |
: Similarly, in the 4<sup>th</sup> group, where larvae are exposed to EA odor paired with electric shock (odor prior to shock), we have: <math>x_o =32</math>, and <math>P(x_o > 32) =0.000056</math>, when <math>x_o \sim Binomial(N = 41, p = 0.5)</math>. Thus, we can reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid it are different (within the '''odor+shock treatment group'''). (Recall that in [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair |this non-parametric inference section we discussed these types of calculations]]). | : Similarly, in the 4<sup>th</sup> group, where larvae are exposed to EA odor paired with electric shock (odor prior to shock), we have: <math>x_o =32</math>, and <math>P(x_o > 32) =0.000056</math>, when <math>x_o \sim Binomial(N = 41, p = 0.5)</math>. Thus, we can reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid it are different (within the '''odor+shock treatment group'''). (Recall that in [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair |this non-parametric inference section we discussed these types of calculations]]). | ||
Current revision as of 21:06, 28 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Contingency Tables: Independence and Homogeneity
Contingency Tables: Independence and Homogeneity
The Chi-Square Test may also be used to assess independence and association between variables.
Motivational example
Suppose 200 randomly selected cancer patients were asked if their primary diagnosis was Brain cancer and if they owned a cell phone before their diagnosis. The results are presented in the table below.
Suppose we want to analyze the association, if any, between brain cancer and cell phone use. The 2x2 table below lists two possible outcomes for each variable (each variable is dichotomous). We have the following population parameters:
- P(CP|BC) = true probability of owning a cell phone (CP) given that the patient had brain cancer (BC). This chance may be estimated by P(CP|BC) = 0.72.
- P(CP|NBC) = true probability of owning a cell phone given that the patient had another cancer, which is estimated by P(CP|NBC) = 0.46
| Brain cancer | ||||
| Yes | No | Total | ||
| Cell Phone Use | Yes | 18 | 80 | 98 |
| No | 7 | 95 | 102 | |
| Total | 25 | 175 | 200 | |
Does it seem like there is an association between brain cancer and cell phone use? Of the brain cancer patients 18/25 = 0.72, owned a cell phone before their diagnosis. P(CP|BC) = 0.72, estimated probability of owning a cell phone given that the patient has brain cancer.
Of the other cancer patients, 80/175 = 0.46, owned a cell phone before their diagnosis. P(CP|NBC) = 0.46, estimated probability of owning a cell phone given that the patient has another cancer.
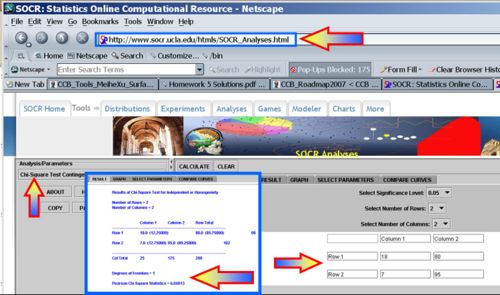
Calculations
- The Hypotheses:
- Ho: There is no association between variable 1 and variable 2 (independence)
- P(BC|CP)=P(BC), that is brain-cancer (BC) is independent of cell-phone (CP) usage.
- Ha: There is an association between variable 1 and variable 2 (dependence)
-
- Test Statistics:
The Test Statistic:
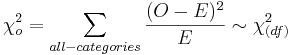 , where df = (# rows – 1)(# columns – 1).
, where df = (# rows – 1)(# columns – 1).
- Expected cell counts can be calculated by
-
- P-values and Critical Values for the Chi-Square Distribution may be easily computed using SOCR Distributions.
- Results:
For the brain-cancer and cell-phone usage data we have:
- P-value:
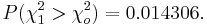 and we can reject the null hypothesis at α = 0.05.
and we can reject the null hypothesis at α = 0.05.
Notes
- CAUTION: Association does not imply Causality!
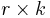 Contingency Tables
Contingency Tables
We now consider tables that are larger than a 2x2 (more than 2 groups or more than 2 categories), called 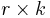 Contingency Tables. The testing procedure is the same as the 2x2 contingency table, just more work and no possibility for a directional alternative. The goal of an
Contingency Tables. The testing procedure is the same as the 2x2 contingency table, just more work and no possibility for a directional alternative. The goal of an 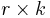 contingency table is to investigate the relationship between the row and column variables
contingency table is to investigate the relationship between the row and column variables
- Note: Ho is a compound hypothesis because it contains more than one independent assertion. This will be true for all
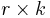 tables larger than 2x2. In other words, the alternative hypothesis for
tables larger than 2x2. In other words, the alternative hypothesis for 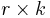 tables larger than 2x2, will always be non-directional.
tables larger than 2x2, will always be non-directional.
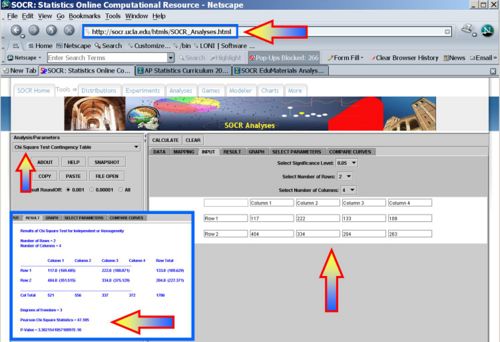
Earthquake Insurance Example
Many factors are considered when purchasing earthquake insurance. One factor of interest may be location with respect to a major earthquake fault. Suppose a survey is mailed to California residents in four counties (data shown below). Is there a statistically significant association between county of residence and purchase of earthquake insurance? Test using a = 0.05.
| County | ||||||
| Contra Costa (CC) | Santa Clara (SC) | Los Angeles (LA) | San Bernardino (SB) | Total | ||
| Earthquake Insurance | Yes | 117 | 222 | 133 | 109 | 581 |
| No | 404 | 334 | 204 | 263 | 1205 | |
| Total | 521 | 556 | 337 | 372 | 1786 | |
- Hypotheses:
- Ho: There is no association between earthquake insurance and county of residence in California. That is:
- P(Y|CC) = P(Y|SC) = P(Y|LA) = P(Y|SB)
- P(N|CC) = P(N|SC) = P(N|LA) = P(N|SB)
- Ha: There is an association between earthquake insurance and county of residence in California. The probability of having earthquake insurance is not the same in each county.
- P-value = 3.302154105710997E-10
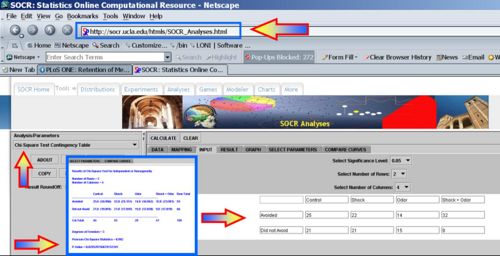
Moths Memory from Caterpillar Stage
One study (Blackiston, Casey and Weiss, 2008) showed that moths can remember something they learned at caterpillar stage -- an association of an odor with an electric shock. This memory remains even though the metamorphosis decomposes much of their entire (caterpillar) body and reconstitutes it again (as a moth).
Tobacco hornworm moth caterpillars were put into one of 4 treatment groups: control, shock, odor, or shock and odor. Then the moths were observed to see whether they avoided the odor. If the moths could "remember" the odor association with shock, then one would expect a greater rate of avoidance of odor in the moths in the last group. The empirical results seem to provide evidence in supporting this hypothesis. This study employed a classical conditioning to train caterpillars to avoid the odor of ethyl acetate (EA) by pairing odor with a mild electric shock. The data are included in the table below.
| Group | ||||||
| Control | Shock | Odor | Shock + Odor | Total | ||
| Odor Avoidance | Avoided Odor | 25 | 22 | 14 | 32 | 93 |
| Did not Avoid Odor | 21 | 21 | 15 | 9 | 66 | |
| Total | 46 | 43 | 29 | 41 | 159 | |
Use the SOCR Chi-square test of association to find out if indeed the data support a research hypothesis that training memory may proliferate through the transition process of metamorphosis from caterpillar to moth. Also establish that the first three groups don't deviate significantly from the (null hypothesis) 50% avoidance level. Therefore, the moths seem naturally unaffected by the odor itself. You can also show that the Shock + Odor treatment group has an avoidance of the odor rate significantly higher than 0.5 (given by the null hypothesis).
- Hypotheses:
- Ho: There is no association between odor avoidance and treatment. That is:
- P(Avoid|Shock+Odor) = P(Avoid|Odor).
- Ha: There is an association between odor avoidance and treatment. The probability of avoiding odor depends on the treatment applied at the larvae stage (before the metamorphosis to moths).
- P-value = 0.029529758678132345 indicates that there is an association between these two variables.
We can also test to see if within each treatment group, there is a strong group separation between the moths that avoided the EA odor and those that did not. Recall that this can be done by the sign-test.
- Controls: xo = 25, and P(xo > 25) = 0.230696, when
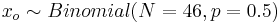 . Thus, we cannot reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid the odor are different (within the Control group).
. Thus, we cannot reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid the odor are different (within the Control group).
- Similarly, in the 4th group, where larvae are exposed to EA odor paired with electric shock (odor prior to shock), we have: xo = 32, and P(xo > 32) = 0.000056, when
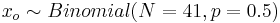 . Thus, we can reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid it are different (within the odor+shock treatment group). (Recall that in this non-parametric inference section we discussed these types of calculations).
. Thus, we can reject a null hypothesis that the proportions of moths that avoided the odor and those that did not avoid it are different (within the odor+shock treatment group). (Recall that in this non-parametric inference section we discussed these types of calculations).
Chi-Square Test Conditions
Conditions for validity of the χ2 test are:
- Design conditions
- for a goodness of fit, it must be reasonable to regard the data as a random sample of categorical observations from a large population.
- for a contingency table, it must be appropriate to view the data in one of the following ways:
- as two or more independent random samples, observed with respect to a categorical variable
- as one random sample, observed with respect to two categorical variables
- for either type of test, the observations within a sample must be independent of one another.
- Sample conditions
- critical values only work if each expected value > 5
Problems
References
- Blackiston DJ, Silva Casey E, Weiss MR (2008) Retention of Memory through Metamorphosis: Can a Moth Remember What It Learned As a Caterpillar? PLoS ONE 3(3): e1736. doi:10.1371/journal.pone.0001736
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: