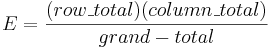AP Statistics Curriculum 2007 Contingency Indep
From Socr
(→Calculations) |
|||
| Line 37: | Line 37: | ||
==Calculations== | ==Calculations== | ||
| - | |||
| - | |||
* The hypotheses: | * The hypotheses: | ||
| Line 48: | Line 46: | ||
The test statistic: | The test statistic: | ||
| - | :<math>\chi_o^2 = \sum_{all-categories}{(O-E)^2 \over E} \sim \chi_{(df=(\ | + | :<math>\chi_o^2 = \sum_{all-categories}{(O-E)^2 \over E} \sim \chi_{(df=(number\_of\_rows – 1)(number\_of_\_columns – 1))}^2</math> |
: Expected cell counts can be calculated by | : Expected cell counts can be calculated by | ||
| - | :: <math>E = { (row | + | :: <math>E = { (row\_total)(column\_total)\over grand-total}</math> |
with ''df = (# rows – 1)(# col – 1)''. | with ''df = (# rows – 1)(# col – 1)''. | ||
Revision as of 02:03, 4 March 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Contingency Tables: Independence and Homogeneity
Contingency Tables: Independence and Homogeneity
The chi-square test may also be used to assess independence and association between variables.
Motivational example
Suppose 200 randomly selected cancer patients were asked if their primary diagnosis was Brain cancer and if they owned a cell phone before their diagnosis. The results are presented in the table below.
Suppose we want to analyze the association, if any, between brain cancer and cell phone use. The 2x2 table below lists two possible outcomes for each variable (each variable is dichotomous). We have the following population parameters:
- P(CP|BC) = true probability of owning a cell phone (CP) given that the patient had brain cancer (BC). This chance may be estimated by P(CP|BC) = 0.72.
- P(CP|NBC) = true probability of owning a cell phone given that the patient had another cancer, which is estimated by P(CP|NBC) = 0.46
| Brain cancer | ||||
| Yes | No | Total | ||
| Cell Phone Use | Yes | 18 | 80 | 98 |
| No | 7 | 95 | 102 | |
| Total | 25 | 175 | 200 | |
Does it seem like there is an association between brain cancer and cell phone use? Of the brain cancer patients 18/25 = 0.72, owned a cell phone before their diagnosis. P(CP|BC) = 0.72, estimated probability of owning a cell phone given that the patient has brain cancer.
Of the other cancer patients, 80/175 = 0.46, owned a cell phone before their diagnosis. P(CP|NBC) = 0.46, estimated probability of owning a cell phone given that the patient has another cancer.
Calculations
- The hypotheses:
- Ho: there is no association between variable 1 and variable 2 (independence)
- Ha: there is an association between variable 1 and variable 2 (dependence)
- Test statistics:
The test statistic:
- Failed to parse (lexing error): \chi_o^2 = \sum_{all-categories}{(O-E)^2 \over E} \sim \chi_{(df=(number\_of\_rows – 1)(number\_of_\_columns – 1))}^2
- Expected cell counts can be calculated by
-
with df = (# rows – 1)(# col – 1).
- P-values and critical values for the Chi-Square distribution may be easily computed using SOCR Distributions.
- Results:
Examples
Applications
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: