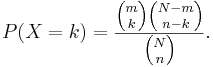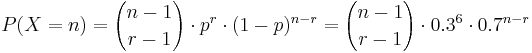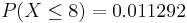AP Statistics Curriculum 2007 Distrib Dists
From Socr
(→Normal approximation to Negative Binomial distribution) |
m (→Normal approximation to Negative Binomial distribution) |
||
| Line 110: | Line 110: | ||
====Normal approximation to Negative Binomial distribution==== | ====Normal approximation to Negative Binomial distribution==== | ||
| - | The central limit theorem applies provides the foundation for approximation of negative binomial distribution by [[AP_Statistics_Curriculum_2007_Normal_Std| Normal distribution]]. Each negative binomial random variable, \(V_k \sim NB(r,p)\), may be expressed as a sum of '''k''' independent, identically distributed ([[AP_Statistics_Curriculum_2007_Distrib_Dists | + | The central limit theorem applies provides the foundation for approximation of negative binomial distribution by [[AP_Statistics_Curriculum_2007_Normal_Std| Normal distribution]]. Each negative binomial random variable, \(V_k \sim NB(r,p)\), may be expressed as a sum of '''k''' independent, identically distributed ([[AP_Statistics_Curriculum_2007_Distrib_Dists|geometric]]) random variables \(\{X_i\}\), i.e., \( V_k = \sum_{i=1}^k{X_i}\), where [[AP_Statistics_Curriculum_2007_Distrib_Dists |\( X_i \sim Geometric(p)\)]]. In various scientific applications, given a large '''k''', the distribution of \(V_k\) is approximately normal with mean and variance given by \(\mu=k\frac{1}{p}\) and \(\sigma^2=k\frac{1-p}{p^2}\), as \(k \longrightarrow \infty\). Depending on the parameter '''p''', '''k''' may need to be rather large for the approximation to work well. Also, when using the normal approximation, we should remember to use the continuity correction, since the negative binomial and Normal distributions are discrete and continuous, respectively. |
In the above example, \(V_k \sim NegBin(k=r=6, p=0.3)\), the normal distribution approximation, \(N(\mu=\frac{k}{p}=20, \sigma=\sqrt{k\frac{1-p}{p^2}}=6.83)\), is shown it the following image and table: | In the above example, \(V_k \sim NegBin(k=r=6, p=0.3)\), the normal distribution approximation, \(N(\mu=\frac{k}{p}=20, \sigma=\sqrt{k\frac{1-p}{p^2}}=6.83)\), is shown it the following image and table: | ||
Revision as of 19:15, 23 June 2012
Contents |
General Advance-Placement (AP) Statistics Curriculum - Geometric, HyperGeometric, Negative Binomial Random Variables and Experiments
Geometric
- Definition: The Geometric Distribution is the probability distribution of the number X of Bernoulli trials needed to get one success, supported on the set {1, 2, 3, ...}. The name geometric is a direct derivative from the mathematical notion of geometric series.
- Mass Function: If the probability of successes on each trial is P(success)=p, then the probability that x trials are needed to get one success is
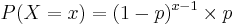 , for x = 1, 2, 3, 4,....
, for x = 1, 2, 3, 4,....
- Expectation: The Expected Value of a geometrically distributed random variable X is
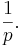 This is because geometric series have this property:
This is because geometric series have this property:
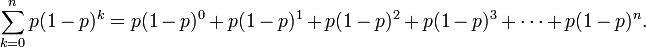
- Let r=(1-p), then p=(1-r) and
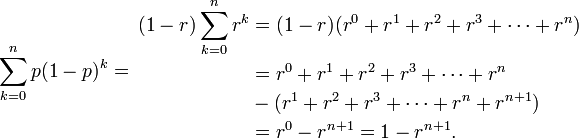
- Thus:
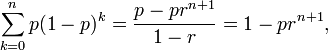 which converges to 1, as
which converges to 1, as 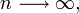 , and hence the above geometric density is well defined.
, and hence the above geometric density is well defined.
- Denote the geometric expectation by E = E(X) =
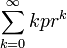 , where r=1-p. Then
, where r=1-p. Then 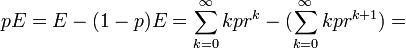
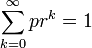 . Therefore,
. Therefore, 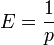 .
.
- Variance: The Variance is
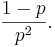
- Example: See this SOCR Geometric distribution activity.
- The Geometric distribution gets its name because its probability mass function is a geometric progression. It is the discrete analogue of the Exponential distribution and is also known as Furry distribution.
HyperGeometric
The hypergeometric distribution is a discrete probability distribution that describes the number of successes in a sequence of n draws from a finite population without replacement. An experimental design for using Hypergeometric distribution is illustrated in this table:
| Type | Drawn | Not-Drawn | Total |
| Defective | k | m-k | m |
| Non-Defective | n-k | N+k-n-m | N-m |
| Total | n | N-n | N |
- Explanation: Suppose there is a shipment of N objects in which m are defective. The Hypergeometric Distribution describes the probability that in a sample of n distinctive objects drawn from the shipment exactly k objects are defective.
- Mass function: The random variable X follows the Hypergeometric Distribution with parameters N, m and n, then the probability of getting exactly k successes is given by
This formula for the Hypergeometric Mass Function may be interpreted as follows: There are 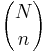 possible samples (without replacement). There are
possible samples (without replacement). There are 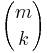 ways to obtain k defective objects and there are
ways to obtain k defective objects and there are 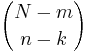 ways to fill out the rest of the sample with non-defective objects.
ways to fill out the rest of the sample with non-defective objects.
The mean and variance of the hypergeometric distribution have the following closed forms:
- Mean:
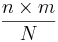
- Variance:
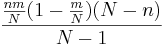
Examples
- SOCR Activity: The SOCR Ball and Urn Experiment provides a hands-on demonstration of the utilization of Hypergeometric distribution in practice. This activity consists of selecting n balls at random from an urn with N balls, R of which are red and the other N - R green. The number of red balls Y in the sample is recorded on each update. The distribution and moments of Y are shown in blue in the distribution graph and are recorded in the distribution table. On each update, the empirical density and moments of Y are shown in red in the distribution graph and are recorded in the distribution table. Either of two sampling models can be selected with the list box: with replacement and without replacement. The parameters N, R, and n can vary with scroll bars.
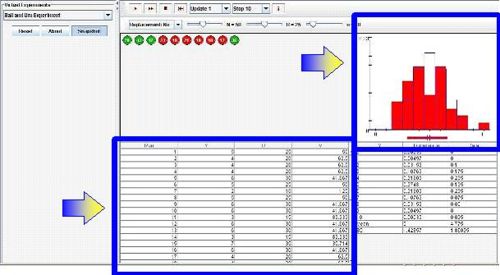
- A lake contains 1,000 fish; 100 are randomly caught and tagged. Suppose that later we catch 20 fish. Use SOCR Hypergeometric Distribution to:
- Compute the probability mass function of the number of tagged fish in the sample of 20.
- Compute the expected value and the variance of the number of tagged fish in this sample.
- Compute the probability that this random sample contains more than 3 tagged fish.
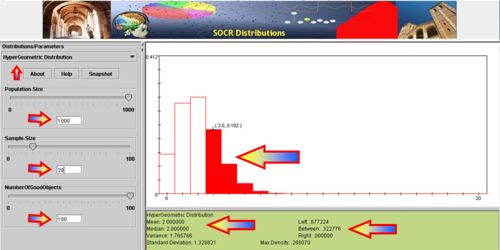
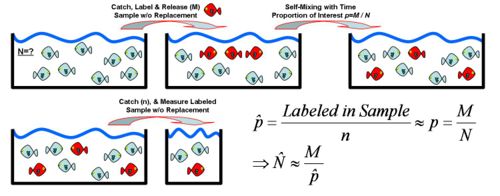
- Hypergeometric distribution may also be used to estimate the population size: Suppose we are interested in determining the population size. Let N = number of fish in a particular isolated region. Suppose we catch, tag and release back M=200 fish. Several days later, when the fish are randomly mixed with the untagged fish, we take a sample of n=100 and observe m=5 tagged fish. Suppose p=200/N is the population proportion of tagged fish. Notice that when sampling fish, we sample without replacement. Thus, hypergeometric is the exact model for this process. Assuming the sample-size (n) is < 5% of the population size(N), we can use binomial approximation to hypergeometric. Thus if the sample of n=100 fish had 5 tagged, the sample-proportion (estimate of the population proportion) will be
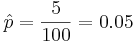 . Thus, we can estimate that
. Thus, we can estimate that 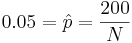 , and
, and 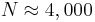 , as shown in the figure below.
, as shown in the figure below.
- You can also see a manual calculation example using the hypergeometric distribution here.
Negative Binomial
The family of Negative Binomial Distributions is a two-parameter family; p and r with 0 < p < 1 and r > 0. There are two (identical) combinatorial interpretations of Negative Binomial processes (X or Y).
X=Trial index (n) of the rth success, or Total # of experiments (n) to get r successes
- Probability Mass Function:
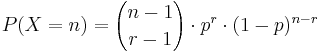 , for n = r,r+1,r+2,.... (n=trial number of the rth success)
, for n = r,r+1,r+2,.... (n=trial number of the rth success)
- Mean:
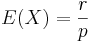
- Variance:
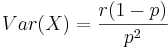
Y = Number of failures (k) to get r successes
- Probability Mass Function:
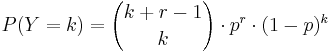 , for k = 0,1,2,.... (k=number of failures before the rth successes)
, for k = 0,1,2,.... (k=number of failures before the rth successes)
-
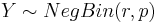 , the probability of k failures and r successes in n=k+r Bernoulli(p) trials with success on the last trial.
, the probability of k failures and r successes in n=k+r Bernoulli(p) trials with success on the last trial.
- Mean:
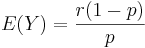 .
.
- Variance:
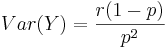 .
.
- Note that X = Y + r, and E(X) = E(Y) + r, whereas VAR(X)=VAR(Y).
SOCR Negative Binomial Experiment
Application
Suppose Jane is promoting and fund-raising for a presidential candidate. She wants to visit all 50 states and she's pledged to get all electoral votes of 6 states before she and the candidate she represents are satisfied. In every state, there is a 30% chance that Jane will be able to secure all electoral votes and a 70% chance that she'll fail.
- What's the probability mass function of the number of failures (k=n-r) to get r=6 successes?
- In other words, what's the probability mass function that the last 6th state she succeeds to secure all electoral votes happens to be at the nth state she campaigns in?
NegBin(r, p) distribution describes the probability of k failures and r successes in n=k+r Bernoulli(p) trials with success on the last trial. Looking to secure the electoral votes for 6 states means Jane needs to get 6 successes before she (and her candidate) is happy. The number of trials (i.e., states visited) needed is n=k+6. The random variable we are interested in is X={number of states visited to achieve 6 successes (secure all electoral votes within these states)}. So, n = k+6, and 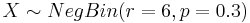 . Thus, for
. Thus, for 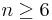 , the mass function (giving the probabilities that Jane will visit n states before her ultimate success is:
, the mass function (giving the probabilities that Jane will visit n states before her ultimate success is:
- What's the probability that Jane finishes her campaign in the 10th state?
- Let
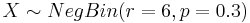 , then
, then 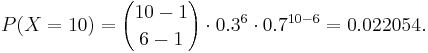
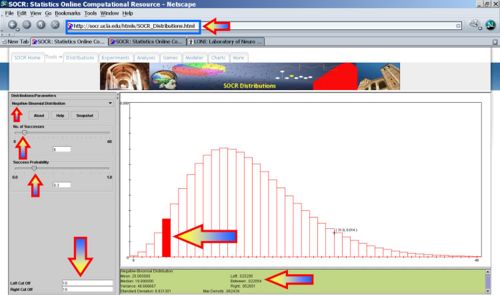
- What's the probability that Jane finishes campaigning on or before reaching the 8th state?
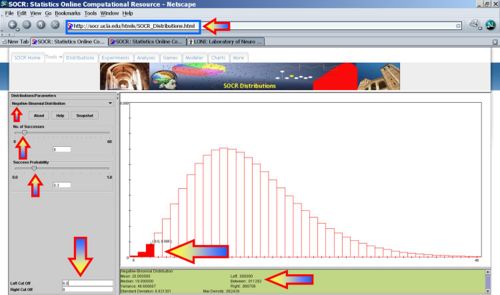
- Suppose the success of getting all electoral votes within a state is reduced to only 10%, then X~NegBin(r=6, p=0.1). Notice that the shape and domain the Negative-Binomial distribution significantly chance now (see image below).
- What's the probability that Jane covers all 50 states but fails to get all electoral votes in any 6 states (as she had hoped for)?
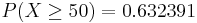
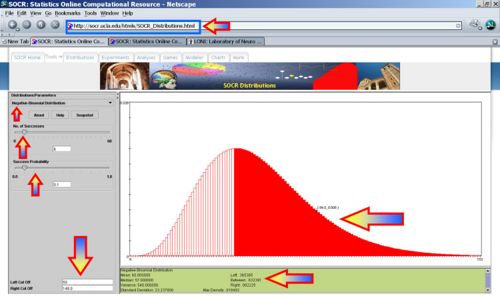
- SOCR Activity: If you want to see an interactive Negative-Binomial Graphical calculator you can go to this applet (select Negative Binomial) and see this activity.
Normal approximation to Negative Binomial distribution
The central limit theorem applies provides the foundation for approximation of negative binomial distribution by Normal distribution. Each negative binomial random variable, \(V_k \sim NB(r,p)\), may be expressed as a sum of k independent, identically distributed (geometric) random variables \(\{X_i\}\), i.e., \( V_k = \sum_{i=1}^k{X_i}\), where \( X_i \sim Geometric(p)\). In various scientific applications, given a large k, the distribution of \(V_k\) is approximately normal with mean and variance given by \(\mu=k\frac{1}{p}\) and \(\sigma^2=k\frac{1-p}{p^2}\), as \(k \longrightarrow \infty\). Depending on the parameter p, k may need to be rather large for the approximation to work well. Also, when using the normal approximation, we should remember to use the continuity correction, since the negative binomial and Normal distributions are discrete and continuous, respectively.
In the above example, \(V_k \sim NegBin(k=r=6, p=0.3)\), the normal distribution approximation, \(N(\mu=\frac{k}{p}=20, \sigma=\sqrt{k\frac{1-p}{p^2}}=6.83)\), is shown it the following image and table:
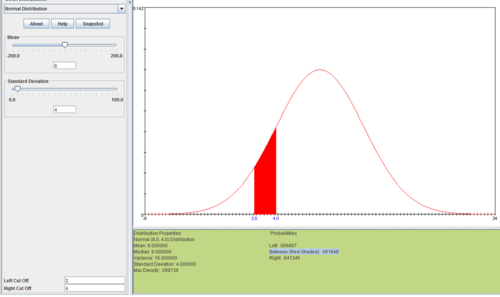
The probabilities of the real Gamma and approximate Normal distributions (on the range [2:4]) are not identical but are sufficiently close.
| Summary | \(\Gamma(k=4, \theta=2)\) | \(Normal(\mu=8, \sigma^2=4)\) |
|---|---|---|
| Mean | 8.000000 | 8.0 |
| Median | 7.32 | 8.0 |
| Variance | 16.0 | 16.0 |
| Standard Deviation | 4.0 | 4.0 |
| Max Density | 0.112021 | 0.099736 |
| Probability Areas | ||
| <2 | 0.018988 | 0.066807 |
| [2:4] | 0.123888 | 0.091848 |
| >4 | 0.857123 | 0.841345 |
Negative Multinomial Distribution (NMD)
The Negative Multinomial Distribution is a generalization of the two-parameter Negative Binomial distribution (NB(r,p)) to 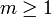 outcomes. Suppose we have an experiment that generates
outcomes. Suppose we have an experiment that generates 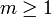 possible outcomes,
possible outcomes, 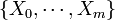 , each occurring with probability
, each occurring with probability 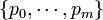 , respectively, where with 0 < pi < 1 and
, respectively, where with 0 < pi < 1 and 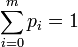 . That is,
. That is, 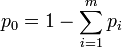 . If the experiment proceeds to generate independent outcomes until
. If the experiment proceeds to generate independent outcomes until 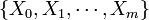 occur exactly
occur exactly 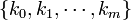 times, then the distribution of the m-tuple
times, then the distribution of the m-tuple 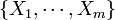 is Negative Multinomial with parameter vector
is Negative Multinomial with parameter vector 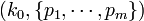 . Notice that the degree-of-freedom here is actually m, not (m+1). That is why we only have a probability parameter vector of size m, not (m+1), as all probabilities add up to 1 (so this introduces one relation). Contrast this with the combinatorial interpretation of Negative Binomial (special case with m=1):
. Notice that the degree-of-freedom here is actually m, not (m+1). That is why we only have a probability parameter vector of size m, not (m+1), as all probabilities add up to 1 (so this introduces one relation). Contrast this with the combinatorial interpretation of Negative Binomial (special case with m=1):
- X˜NegativeBinomial(NumberOfSuccesses = r,ProbOfSuccess = p),
- X=Total # of experiments (n) to get r successes (and therefore n-r failures);
- X˜NegativeMultinomial(k0,{p0,p1}),
- X=Total # of experiments (n) to get k0 (default variable, Xo) and n − k0 outcomes of the other possible outcome (X1).
Negative Multinomial Summary
- Probability Mass Function:
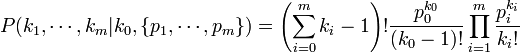 , or equivalently:
, or equivalently:
-
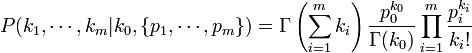 , where Γ(x) is the Gamma function.
, where Γ(x) is the Gamma function.
- Mean (vector):
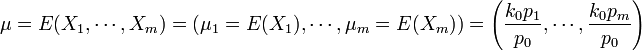 .
.
- Variance-Covariance (matrix): Cov(Xi,Xj) = {cov[i,j]}, where
-
![cov[i,j] = \begin{cases} \frac{k_0 p_i p_j}{p_0^2},& i\not= j,\\
\frac{k_0 p_i (p_i + p_0)}{p_0^2},& i=j.\end{cases}](/socr/uploads/math/5/b/1/5b1d1f58c8f8acdb3160b06a5d21f676.png) .
.
Cancer Example
The Probability Theory Chapter of the EBook shows the following example using 400 Melanoma (skin cancer) Patients where the Type and Site of the cancer are recorded for each subject, as shown in the Table below.
| Type | Site | Totals | ||
| Head and Neck | Trunk | Extremities | ||
| Hutchinson's melanomic freckle | 22 | 2 | 10 | 34 |
| Superficial | 16 | 54 | 115 | 185 |
| Nodular | 19 | 33 | 73 | 125 |
| Indeterminant | 11 | 17 | 28 | 56 |
| Column Totals | 68 | 106 | 226 | 400 |
The sites (locations) of the cancer may be independent, but there may be positive dependencies of the type of cancer for a given location (site). For example, localized exposure to radiation implies that elevated level of one type of cancer (at a given location) may indicate higher level of another cancer type at the same location. We want to use the Negative Multinomial distribution to model the sites cancer rates and try to measure some of the cancer type dependencies within each location.
Let's denote by xi,j the cancer rates for each site ( ) and each type of cancer (
) and each type of cancer ( ). For each (fixed) site (
). For each (fixed) site (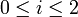 ), the cancer rates are independent Negative Multinomial distributed random variables. That is, for each column index (site) the column-vector X has the following distribution:
), the cancer rates are independent Negative Multinomial distributed random variables. That is, for each column index (site) the column-vector X has the following distribution:
- X = {X1,X2,X3}˜NMD(k0,{p1,p2,p3}).
Different columns (sites) are considered to be different instances of the random negative-multinomially distributed vector, X. Then we have the following estimates:
- MLE estimate of the Mean: is given by:
-
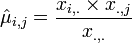
-
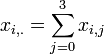
-
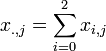
-
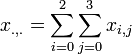
- Example:
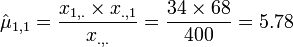
-
- Variance-Covariance: For a single column vector, X = {X1,X2,X3}˜NMD(k0,{p1,p2,p3}), covariance between any pair of Negative Multinomial counts (Xi and Xj) is:
-
![cov[X_i,X_j] = \begin{cases} \frac{k_0 p_i p_j}{p_0^2},& i\not= j,\\
\frac{k_0 p_i (p_i + p_0)}{p_0^2},& i=j.\end{cases}](/socr/uploads/math/d/5/7/d57451e51192ed46d4a946d90e25990a.png) .
.
- Example: For the first site (Head and Neck, j=0), suppose that
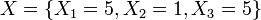 and X˜NMD(k0 = 10,{p1 = 0.2,p2 = 0.1,p3 = 0.2}). Then:
and X˜NMD(k0 = 10,{p1 = 0.2,p2 = 0.1,p3 = 0.2}). Then:
-
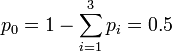
- NMD(X | k0,{p1,p2,p3}) = 0.00465585119998784
-
![cov[X_1,X_3] = \frac{10 \times 0.2 \times 0.2}{0.5^2}=1.6](/socr/uploads/math/3/8/5/3856250206cbbc14e0a5711c107d924f.png)
-
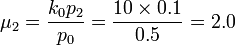
-
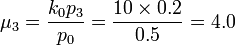
-
![corr[X_2,X_3] = \left (\frac{\mu_2 \times \mu_3}{(k_0+\mu_2)(k_0+\mu_3)} \right )^{\frac{1}{2}}](/socr/uploads/math/8/a/0/8a0eed030df471cf1d24d18932b436c4.png) and therefore,
and therefore, ![corr[X_2,X_3] = \left (\frac{2 \times 4}{(10+2)(10+4)} \right )^{\frac{1}{2}} = 0.21821789023599242.](/socr/uploads/math/9/3/6/936f6ecdb9cfbd2dc64f7c0d874ed47d.png)
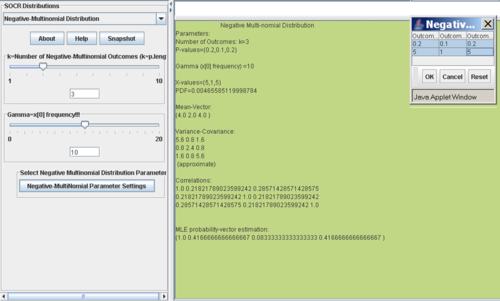
- You can also use the interactive SOCR negative multinomial distribution calculator to compute these quantities, as shown on the figure below.
- Example: For the first site (Head and Neck, j=0), suppose that
- There is no MLE estimate for the NMD k0 parameter (see this reference). However, there are approximate protocols for estimating the k0 parameter, see the example below.
- Correlation: correlation between any pair of Negative Multinomial counts (Xi and Xj) is:
-
![Corr[X_i,X_j] = \begin{cases} \left (\frac{\mu_i \times \mu_j}{(k_0+\mu_i)(k_0+\mu_j)} \right )^{\frac{1}{2}} =
\left (\frac{p_i p_j}{(p_0+p_i)(p_0+p_j)} \right )^{\frac{1}{2}}, & i\not= j, \\
1, & i=j.\end{cases}](/socr/uploads/math/e/9/1/e912270fcb0cb37bed2b36277547fda9.png) .
.
- The marginal distribution of each of the Xi variables is negative binomial, as the Xi count (considered as success) is measured against all the other outcomes (failure). But jointly, the distribution of
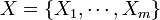 is negative multinomial, i.e.,
is negative multinomial, i.e., 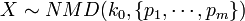 .
.
Notice that the pair-wise NMD correlations are always positive, where as the correlations between multinomail counts are always negative. Also note that as the parameter k0 increases, the paired correlations go to zero! Thus, for large k0, the Negative Multinomial counts Xi behave as independent Poisson random variables with respect to their means 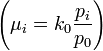 .
.
Parameter estimation
- Estimation of the mean (expected) frequency counts (μj) of each outcome (Xj):
- The MLE estimates of the NMD mean parameters μj are easy to compute.
- If we have a single observation vector
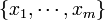 , then
, then 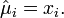
- If we have several observation vectors, like in this case we have the cancer type frequencies for 3 different sites, then the MLE estimates of the mean counts are
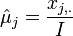 , where
, where 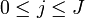 is the cancer-type index and the summation is over the number of observed (sampled) vectors (I).
is the cancer-type index and the summation is over the number of observed (sampled) vectors (I).
- For the cancer data above, we have the following MLE estimates for the expectations for the frequency counts:
- Hutchinson's melanomic freckle type of cancer (X0) is
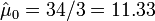 .
.
- Superficial type of cancer (X1) is
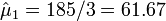 .
.
- Nodular type of cancer (X2) is
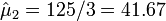 .
.
- Indeterminant type of cancer (X3) is
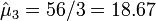 .
.
- Hutchinson's melanomic freckle type of cancer (X0) is
- If we have a single observation vector
- Estimation of the k0 (gamma) parameter:
- There is no MLE for the k0 parameter; however, there is a protocol for estimating k0 using the chi-squared goodness of fit statistic. In the usual chi-squared statistic:
-
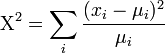 , we can replace the expected-means (μi) by their estimates,
, we can replace the expected-means (μi) by their estimates, 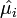 , and replace denominators by the corresponding negative multinomial variances. Then we get the following test statistic for negative multinomial distributed data:
, and replace denominators by the corresponding negative multinomial variances. Then we get the following test statistic for negative multinomial distributed data:
-
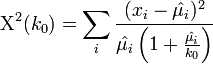 .
.
- Now we can derive a simple method for estimating the k0 parameter by varying the values of k0 in the expression Χ2(k0) and matching the values of this statistic with the corresponding asymptotic chi-squared distribution. The following protocol summarizes these steps using the cancer data above:
- DF: The degree of freedom for the Chi-square distribution in this case is:
- df = (# rows – 1)(# columns – 1) = (3-1)*(4-1) = 6
- Median: The median of a chi-squared random variable with 6 df is 5.261948.
- Mean Counts Estimates: The mean counts estimates (μj) for the 4 different cancer types are:
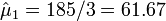 ;
; 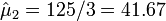 ; and
; and 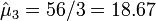 .
.
- Thus, we can solve the equation above Χ2(k0) = 5.261948 for the single variable of interest -- the unknown parameter k0. Suppose we are using the same example as before, x = {x1 = 5,x2 = 1,x3 = 5}. Then the solution is an asymptotic chi-squared distribution driven estimate of the parameter k0.
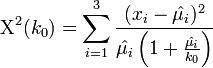 .
.
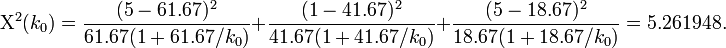 Solving this equation for k0 provides the desired estimate for the last parameter.
Solving this equation for k0 provides the desired estimate for the last parameter.
- Mathematica provides 3 distinct (k0) solutions to this equation: {50.5466, -21.5204, 2.40461}. Since k0 > 0 there are 2 candidate solutions.
- Estimates of Probabilities: Assume k0 = 2 and
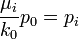 , we have:
, we have:
-
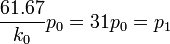
- 20p0 = p2
- 9p0 = p3
- Hence, 1 − p0 = p1 + p2 + p3 = 60p0. Therefore,
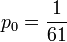 ,
, 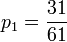 ,
, 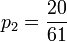 and
and 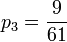 .
.
- Therefore, the best model distribution for the observed sample x = {x1 = 5,x2 = 1,x3 = 5} is
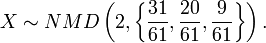
- Notice that in this calculation, we explicitly used the complete cancer data table, not only the sample x = {x1 = 5,x2 = 1,x3 = 5}, as we need multiple samples (multiple sites or columns) to estimate the k0 parameter.
SOCR Negative Multinomial Distribution Calculator
Problems
References
- Negative-Binomial Activity
- Le Gall, F. The modes of a negative multinomial distribution, Statistics & Probability Letters, 2005.
- Johnson et al., 1997 Johnson, N.L., Kotz, S., Balakrishnan, N., 1997. Discrete Multivariate Distributions. Wiley Series in Probability and Mathematical Statistics.
- Kotz and Johnson, 1982 In: S. Kotz and N.L. Johnson, Editors, Encyclopedia of Statistical Sciences, Wiley, New York (1982).
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: