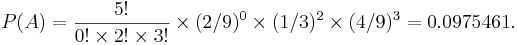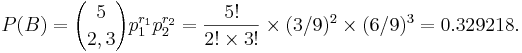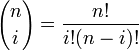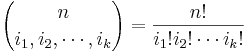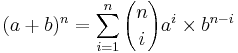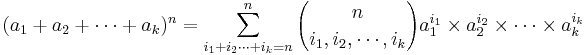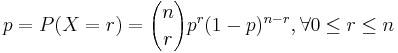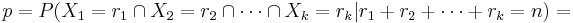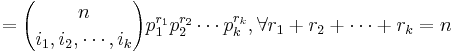AP Statistics Curriculum 2007 Distrib Multinomial
From Socr
m (→Examples of Multinomial experiments) |
|||
| (34 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Multinomial Random Variables and Experiments== | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Multinomial Random Variables and Experiments== | ||
| - | The multinomial experiments (and multinomial | + | The multinomial experiments (and multinomial distributions) directly extend their [[AP_Statistics_Curriculum_2007_Distrib_Binomial |bi-nomial counterparts]]. |
| - | + | ===Multinomial experiments=== | |
| - | ** | + | A multinomial experiment is an experiment that has the following properties: |
| + | * The experiment consists of '''k repeated trials'''. | ||
| + | * Each trial has a '''discrete''' number of possible outcomes. | ||
| + | * On any given trial, the probability that a particular outcome will occur is '''constant'''. | ||
| + | * The trials are '''independent'''; that is, the outcome on one trial does not affect the outcome on other trials. | ||
| - | + | ====Examples of Multinomial experiments==== | |
| - | + | * Suppose we have an urn containing 9 marbles. Two are red, three are green, and four are blue (2+3+4=9). We randomly select 5 marbles from the urn, ''with replacement''. What is the probability (''P(A)'') of the event ''A={selecting 2 green marbles and 3 blue marbles}''? | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | *To solve this problem, we apply the multinomial formula, we know the following: | |
| - | + | ** The experiment consists of 5 trials, so k = 5. | |
| - | + | ** The 5 trials produce 0 red, 2 green marbles, and 3 blue marbles; so <math>r_1=r_{red} = 0</math>, <math>r_2=r_{green} = 2</math>, and <math>r_3=r_{blue} = 3</math>. | |
| + | ** For any particular trial, the probability of drawing a red, green, or blue marble is 2/9, 3/9, and 4/9, respectively. Hence, <math>p_1=p_{red} = 2/9</math>, <math>p_2=p_{green} = 1/3</math>, and <math>p_3=p_{blue} = 4/9</math>. | ||
| + | |||
| + | Plugging these values into the multinomial formula we get the probability of the event of interest to be: | ||
| + | |||
| + | : \(P(A) = {5\choose r_1,r_2,r_3}p_1^{r_1}p_2^{r_2}p_3^{r_3}\). In this specific case, \(P(A) = {5\choose 0,2,3}p_1^{0}p_2^{2}p_3^{3}\). | ||
| + | |||
| + | : <math>P(A) = {5! \over 0!\times 2! \times 3! }\times (2/9)^0 \times (1/3)^2\times (4/9)^3=0.0975461.</math> | ||
| + | |||
| + | Thus, if we draw 5 marbles with replacement from the urn, the probability of drawing no red, 2 green, and 3 blue marbles is ''0.0975461''. | ||
| + | |||
| + | * Let's again use the urn containing 9 marbles, where the number of red, green and blue marbles are 2, 3 and 4, respectively. This time we select 5 marbles from the urn, but are interested in the probability (''P(B)'') of the event ''B={selecting 2 green marbles}''! (Note that 2 < 5) | ||
| + | **To solve this problem, we classify balls into '''green''' and '''others'''! Thus the multinomial experiment consists of 5 trials (k = 5), <math>r_1=r_{green} = 2</math>, <math>r_2=r_{other} = 3</math>. In this case, the probabilities of drawing a '''green''' or '''other''' marble are 3/9, and 6/9, respectively. Notice now the P('''other''') is the sum of the probabilities of the '''other''' colors (complement of green)! Hence, | ||
| + | : <math>P(B) = {5\choose 2, 3}p_1^{r_1}p_2^{r_2} = {5! \over 2! \times 3! }\times (3/9)^2 \times (6/9)^3=0.329218.</math> | ||
| + | |||
| + | This probability is equivalent to the binomial probability (success=green; failure=other color), ''B(n=5, p=1/3)''. | ||
===Synergies between Binomial and Multinomial processes/probabilities/coefficients=== | ===Synergies between Binomial and Multinomial processes/probabilities/coefficients=== | ||
| - | * The Binomial vs. Multinomial '''Coefficients''' | + | * The Binomial vs. Multinomial '''Coefficients''' (See this [http://www.ohrt.com/odds/binomial.php Binomial Calculator]) |
| - | : <math>{n\choose i}=\frac{n!}{ | + | : <math>{n\choose i}=\frac{n!}{i!(n-i)!}</math> |
: <math>{n\choose i_1,i_2,\cdots, i_k}= \frac{n!}{i_1! i_2! \cdots i_k!}</math> | : <math>{n\choose i_1,i_2,\cdots, i_k}= \frac{n!}{i_1! i_2! \cdots i_k!}</math> | ||
* The Binomial vs. Multinomial '''Formulas''' | * The Binomial vs. Multinomial '''Formulas''' | ||
| - | : <math>(a+b)^n = \sum_{i=1}^n{{n\choose i}a^ | + | : <math>(a+b)^n = \sum_{i=1}^n{{n\choose i}a^i \times b^{n-i}}</math> |
: <math>(a_1+a_2+\cdots +a_k)^n = \sum_{i_1+i_2\cdots +i_k=n}^n{ {n\choose i_1,i_2,\cdots, i_k} | : <math>(a_1+a_2+\cdots +a_k)^n = \sum_{i_1+i_2\cdots +i_k=n}^n{ {n\choose i_1,i_2,\cdots, i_k} | ||
a_1^{i_1} \times a_2^{i_2} \times \cdots \times a_k^{i_k}}</math> | a_1^{i_1} \times a_2^{i_2} \times \cdots \times a_k^{i_k}}</math> | ||
| - | * The Binomial vs. Multinomial '''Probabilities''' | + | * The Binomial vs. Multinomial '''Probabilities''' (See this [http://socr.ucla.edu/Applets.dir/Normal_T_Chi2_F_Tables.htm Binomial distribution calculator] and the [http://socr.ucla.edu/htmls/dist/Multinomial_Distribution.html SOCR Multinomial Distribution calculator]) |
| - | : <math>p=P(X=r)={n\choose | + | : <math>p=P(X=r)={n\choose r}p^r(1-p)^{n-r}, \forall 0\leq r \leq n</math> |
| - | : <math>p=P(X_1=r_1 \cap | + | : <math>p=P(X_1=r_1 \cap X_2=r_2 \cap \cdots \cap X_k=r_k | r_1+r_2+\cdots+r_k=n)=</math> |
| + | : <math>={n\choose i_1,i_2,\cdots, i_k}p_1^{r_1}p_2^{r_2}\cdots p_k^{r_k}, \forall r_1+r_2+\cdots+r_k=n</math> | ||
| + | ===Expectation and variance=== | ||
| + | The expected number of times for observing the outcome ''i'', over ''n'' trials, is | ||
| + | :<math>E(X_i) = n p_i.</math> | ||
| - | + | Since each diagonal entry is the variance of a binomially distributed random variable, the [[AP_Statistics_Curriculum_2007_Distrib_MeanVar#Properties_of_Variance | variance-covariance matrix]] is defined by: | |
| - | + | : Diagonal-terms (variances): <math>VAR(X_i)=np_i(1-p_i)</math>, for each ''i'', and | |
| + | : Off-diagonal terms (covariances): <math>COV(X_i,X_j)=-np_i p_j</math>, for <math>i\not= j</math>. | ||
| - | === | + | ===Example=== |
| - | + | Suppose we study N independent trials with results falling in one of k possible categories labeled <math>1,2, \cdots, k</math>. Let <math>p_i</math> be the probability of a trial resulting in the <math>i^{th}</math> category, where <math>p_1+p_2+ \cdots +p_k = 1</math>. Let <math>N_i</math> be the number of trials resulting in the <math>i^{th}</math> category, where <math>N_1+N_2+ \cdots +N_k = N</math>. | |
| + | |||
| + | For instance, suppose we have 9 people arriving at a meeting according to the following information: | ||
| + | : P(by Air) = 0.4, P(by Bus) = 0.2, P(by Automobile) = 0.3, P(by Train) = 0.1 | ||
| + | |||
| + | * Compute the following probabilities | ||
| + | : P(3 by Air, 3 by Bus, 1 by Auto, 2 by Train) = ? | ||
| + | : P(2 by air) = ? | ||
| + | |||
| + | ===SOCR Multinomial Examples=== | ||
| + | Suppose we roll 10 loaded hexagonal (6-face) dice 8 times and we are interested in the probability of observing the event A={3 ones, 3 twos, 2 threes, and 2 fours}. Assume the dice are loaded to the small outcomes according to the following probabilities of the 6 outcomes (''one'' is the most likely and ''six'' is the least likely outcome). | ||
<center> | <center> | ||
{| class="wikitable" style="text-align:center; width:75%" border="1" | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
|- | |- | ||
| - | | x | + | | ''x'' || 1 || 2 || 3 || 4 || 5 || 6 |
|- | |- | ||
| - | | P(X=x) || 0. | + | | ''P(X=x)'' || 0.286 || 0.238 || 0.19 || 0.143 || 0.095 || 0.048 |
|} | |} | ||
</center> | </center> | ||
| - | + | : ''P(A)=?'' Note that the complete description of the event of interest is: | |
| - | + | : A={3 ones, 3 twos, 2 threes, 2 fours, and 0 others (5's or 6's!)} | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | ==== | + | ====Exact Solution==== |
| - | + | Of course, we can compute this probability exactly: | |
| - | * | + | * By-hand calculations: |
| + | : <math>P(A) = {10! \over 3!\times 3! \times 2! \times 2! \times 0! \times 0!} \times 0.286^3 \times 0.238^3\times 0.19^2 \times 0.143^2 \times 0.095^0 \times 0.048^0= </math> | ||
| + | :<math>=0.00586690138260962656816896.</math> | ||
| - | + | * Using the [http://socr.ucla.edu/htmls/dist/Multinomial_Distribution.html SOCR Multinomial Distribution Calculator]: Enter the above given information in the [http://socr.ucla.edu/htmls/dist/Multinomial_Distribution.html SOCR Multimonial distribution applet] to get the probability density and cumulative distribution values for the given outcome ''{3,3,2,2,0}'', as shown on the image below. Note that since the event A does not contain the die outcomes of 5 or 6 , we can reduce the case of 6 outcomes <math>\{1,2,3,4,5,6 \}</math> to a case of 5 outcomes <math>\{1,2,3,4,other \}</math> with corresponding probabilities <math>\{0.286, 0.238, 0.19, 0.143, 0.143 \}</math>, where we pool together the probabilities of the die outcomes of 5 and 6, i.e., P(other)=0.095+0.048=0.143. | |
| - | + | ||
| - | + | <center>[[Image:SOCR_EBook_Dinov_Multinimial_102209_Fig2.png|500px]]</center> | |
| - | === | + | ====Approximate Solution==== |
| - | + | We can also find a pretty close empirically-driven estimate using the [[SOCR_EduMaterials_Activities_DiceExperiment | SOCR Dice Experiment]]. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | For instance, running the [http://socr.ucla.edu/htmls/SOCR_Experiments.html SOCR Dice Experiment] 1,000 times with number of dice n=10, and the loading probabilities listed above, we get an output like the one shown below. | |
| - | + | ||
| - | + | ||
| - | + | <center>[[Image:SOCR_EBook_Dinov_Multinimial_030508_Fig1.jpg|500px]]</center> | |
| - | + | ||
| - | + | ||
| - | + | Now, we can actually count how many of these 1,000 trials generated the event ''A'' as an outcome. In one such experiment of 1,000 trials, there were 8 outcomes of the type {3 ones, 3 twos, 2 threes and 2 fours}. Therefore, the relative proportion of these outcomes to 1,000 will give us a fairly accurate estimate of the exact probability we computed above | |
| - | + | : <math>P(A) \approx {8 \over 1,000}=0.008</math>. | |
| - | + | Note that this approximation is close to the exact answer above. By the [[AP_Statistics_Curriculum_2007_Limits_LLN | Law of Large Numbers (LLN)]], we know that this SOCR empirical compared to the exact multinomial probability of interest will significantly improve as we increase the number of trials in this experiment to 10,000. | |
| - | + | ===[[EBook_Problems_Distrib_Multinomial|Problems]]=== | |
| - | === | + | ===See also=== |
| + | * [[AP_Statistics_Curriculum_2007_Distrib_Dists| Negative Binomial and other Distributions]] | ||
| + | * [[AP_Statistics_Curriculum_2007_Distrib_Dists#Negative_Multinomial_Distribution_.28NMD.29| Negative Multinomial Distribution]] | ||
<hr> | <hr> | ||
Current revision as of 01:35, 17 April 2013
Contents |
General Advance-Placement (AP) Statistics Curriculum - Multinomial Random Variables and Experiments
The multinomial experiments (and multinomial distributions) directly extend their bi-nomial counterparts.
Multinomial experiments
A multinomial experiment is an experiment that has the following properties:
- The experiment consists of k repeated trials.
- Each trial has a discrete number of possible outcomes.
- On any given trial, the probability that a particular outcome will occur is constant.
- The trials are independent; that is, the outcome on one trial does not affect the outcome on other trials.
Examples of Multinomial experiments
- Suppose we have an urn containing 9 marbles. Two are red, three are green, and four are blue (2+3+4=9). We randomly select 5 marbles from the urn, with replacement. What is the probability (P(A)) of the event A={selecting 2 green marbles and 3 blue marbles}?
- To solve this problem, we apply the multinomial formula, we know the following:
- The experiment consists of 5 trials, so k = 5.
- The 5 trials produce 0 red, 2 green marbles, and 3 blue marbles; so r1 = rred = 0, r2 = rgreen = 2, and r3 = rblue = 3.
- For any particular trial, the probability of drawing a red, green, or blue marble is 2/9, 3/9, and 4/9, respectively. Hence, p1 = pred = 2 / 9, p2 = pgreen = 1 / 3, and p3 = pblue = 4 / 9.
Plugging these values into the multinomial formula we get the probability of the event of interest to be:
- \(P(A) = {5\choose r_1,r_2,r_3}p_1^{r_1}p_2^{r_2}p_3^{r_3}\). In this specific case, \(P(A) = {5\choose 0,2,3}p_1^{0}p_2^{2}p_3^{3}\).
Thus, if we draw 5 marbles with replacement from the urn, the probability of drawing no red, 2 green, and 3 blue marbles is 0.0975461.
- Let's again use the urn containing 9 marbles, where the number of red, green and blue marbles are 2, 3 and 4, respectively. This time we select 5 marbles from the urn, but are interested in the probability (P(B)) of the event B={selecting 2 green marbles}! (Note that 2 < 5)
- To solve this problem, we classify balls into green and others! Thus the multinomial experiment consists of 5 trials (k = 5), r1 = rgreen = 2, r2 = rother = 3. In this case, the probabilities of drawing a green or other marble are 3/9, and 6/9, respectively. Notice now the P(other) is the sum of the probabilities of the other colors (complement of green)! Hence,
This probability is equivalent to the binomial probability (success=green; failure=other color), B(n=5, p=1/3).
Synergies between Binomial and Multinomial processes/probabilities/coefficients
- The Binomial vs. Multinomial Coefficients (See this Binomial Calculator)
- The Binomial vs. Multinomial Formulas
- The Binomial vs. Multinomial Probabilities (See this Binomial distribution calculator and the SOCR Multinomial Distribution calculator)
Expectation and variance
The expected number of times for observing the outcome i, over n trials, is
- E(Xi) = npi.
Since each diagonal entry is the variance of a binomially distributed random variable, the variance-covariance matrix is defined by:
- Diagonal-terms (variances): VAR(Xi) = npi(1 − pi), for each i, and
- Off-diagonal terms (covariances): COV(Xi,Xj) = − npipj, for
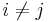 .
.
Example
Suppose we study N independent trials with results falling in one of k possible categories labeled 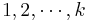 . Let pi be the probability of a trial resulting in the ith category, where
. Let pi be the probability of a trial resulting in the ith category, where 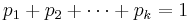 . Let Ni be the number of trials resulting in the ith category, where
. Let Ni be the number of trials resulting in the ith category, where  .
.
For instance, suppose we have 9 people arriving at a meeting according to the following information:
- P(by Air) = 0.4, P(by Bus) = 0.2, P(by Automobile) = 0.3, P(by Train) = 0.1
- Compute the following probabilities
- P(3 by Air, 3 by Bus, 1 by Auto, 2 by Train) = ?
- P(2 by air) = ?
SOCR Multinomial Examples
Suppose we roll 10 loaded hexagonal (6-face) dice 8 times and we are interested in the probability of observing the event A={3 ones, 3 twos, 2 threes, and 2 fours}. Assume the dice are loaded to the small outcomes according to the following probabilities of the 6 outcomes (one is the most likely and six is the least likely outcome).
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X=x) | 0.286 | 0.238 | 0.19 | 0.143 | 0.095 | 0.048 |
- P(A)=? Note that the complete description of the event of interest is:
- A={3 ones, 3 twos, 2 threes, 2 fours, and 0 others (5's or 6's!)}
Exact Solution
Of course, we can compute this probability exactly:
- By-hand calculations:
-
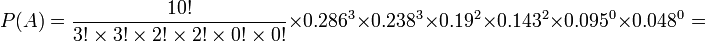
- = 0.00586690138260962656816896.
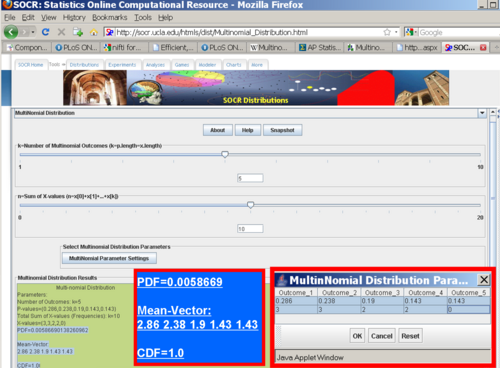
- Using the SOCR Multinomial Distribution Calculator: Enter the above given information in the SOCR Multimonial distribution applet to get the probability density and cumulative distribution values for the given outcome {3,3,2,2,0}, as shown on the image below. Note that since the event A does not contain the die outcomes of 5 or 6 , we can reduce the case of 6 outcomes {1,2,3,4,5,6} to a case of 5 outcomes {1,2,3,4,other} with corresponding probabilities {0.286,0.238,0.19,0.143,0.143}, where we pool together the probabilities of the die outcomes of 5 and 6, i.e., P(other)=0.095+0.048=0.143.
Approximate Solution
We can also find a pretty close empirically-driven estimate using the SOCR Dice Experiment.
For instance, running the SOCR Dice Experiment 1,000 times with number of dice n=10, and the loading probabilities listed above, we get an output like the one shown below.
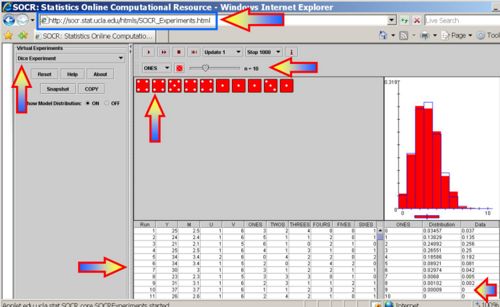
Now, we can actually count how many of these 1,000 trials generated the event A as an outcome. In one such experiment of 1,000 trials, there were 8 outcomes of the type {3 ones, 3 twos, 2 threes and 2 fours}. Therefore, the relative proportion of these outcomes to 1,000 will give us a fairly accurate estimate of the exact probability we computed above
-
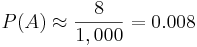 .
.
Note that this approximation is close to the exact answer above. By the Law of Large Numbers (LLN), we know that this SOCR empirical compared to the exact multinomial probability of interest will significantly improve as we increase the number of trials in this experiment to 10,000.
Problems
See also
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: