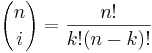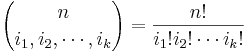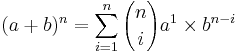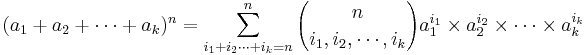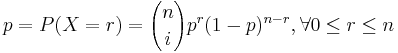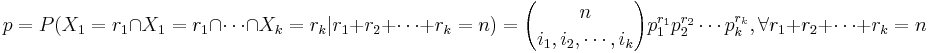AP Statistics Curriculum 2007 Distrib Multinomial
From Socr
(New page: == General Advance-Placement (AP) Statistics Curriculum - Multinomial Random Variables and Experiments== The multinomial experiments (and multinomial di...) |
|||
| Line 4: | Line 4: | ||
* Examples of Multinomial experiments | * Examples of Multinomial experiments | ||
| - | ** Rolling a hexagonal Die 5 times: Where the outcome space is the colection of 5-tuples, where each element is a <math>1\leq value\leq 6</math>. | + | ** Rolling a hexagonal Die 5 times: Where the outcome space is the colection of 5-tuples, where each element is a value such that: <math>1\leq value\leq 6</math>. |
| - | * The Multinomial random variable (RV): Mathematically, a (k) multinomial trial is modeled by a random variable <math>X(outcome) = \begin{cases}x_o,\\ | + | * The Multinomial random variable (RV): Mathematically, a (k) multinomial trial is modeled by a random variable |
| + | <center><math>X(outcome) = \begin{cases}x_o,\\ | ||
x_1,\\ | x_1,\\ | ||
\cdots,\\ | \cdots,\\ | ||
| - | x_k.\end{cases}</math> | + | x_k.\end{cases}</math></center> |
| - | If <math>p_i=P(X= | + | If <math>p_i=P(X=x_i)</math>, then: |
: ''expected value'' of X, <math>E[X]=\sum_{i=1}^k{x_i\times p_i}</math>. | : ''expected value'' of X, <math>E[X]=\sum_{i=1}^k{x_i\times p_i}</math>. | ||
| - | : standard deviation of X, <math>SD[X]=\sqrt{\sum_{i=1}^k{(x_i-E[X | + | : standard deviation of X, <math>SD[X]=\sqrt{\sum_{i=1}^k{(x_i-E[X])^2\times p_i}}</math>. |
===Synergies between Binomial and Multinomial processes/probabilities/coefficients=== | ===Synergies between Binomial and Multinomial processes/probabilities/coefficients=== | ||
* The Binomial vs. Multinomial '''Coefficients''' | * The Binomial vs. Multinomial '''Coefficients''' | ||
| - | : <math> | + | : <math>{n\choose i}=\frac{n!}{k!(n-k)!}</math> |
: <math>{n\choose i_1,i_2,\cdots, i_k}= \frac{n!}{i_1! i_2! \cdots i_k!}</math> | : <math>{n\choose i_1,i_2,\cdots, i_k}= \frac{n!}{i_1! i_2! \cdots i_k!}</math> | ||
| Line 28: | Line 29: | ||
* The Binomial vs. Multinomial '''Probabilities''' | * The Binomial vs. Multinomial '''Probabilities''' | ||
| + | : <math>p=P(X=r)={n\choose i}p^r(1-p)^{n-r}, \forall 0\leq r \leq n</math> | ||
| + | : <math>p=P(X_1=r_1 \cap X_1=r_1 \cap \cdots \cap X_k=r_k | r_1+r_2+\cdots+r_k=n)={n\choose i_1,i_2,\cdots, i_k}p_1^{r_1}p_2^{r_2}\cdots p_k^{r_k}, \forall r_1+r_2+\cdots+r_k=n</math> | ||
| + | |||
===Binomial Random Variables=== | ===Binomial Random Variables=== | ||
Revision as of 23:25, 4 March 2008
Contents
|
General Advance-Placement (AP) Statistics Curriculum - Multinomial Random Variables and Experiments
The multinomial experiments (and multinomial distribtuions) directly extend the their bi-nomial counterparts.
- Examples of Multinomial experiments
- Rolling a hexagonal Die 5 times: Where the outcome space is the colection of 5-tuples, where each element is a value such that:
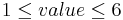 .
.
- Rolling a hexagonal Die 5 times: Where the outcome space is the colection of 5-tuples, where each element is a value such that:
- The Multinomial random variable (RV): Mathematically, a (k) multinomial trial is modeled by a random variable
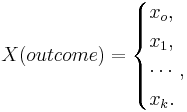
If pi = P(X = xi), then:
- expected value of X,
![E[X]=\sum_{i=1}^k{x_i\times p_i}](/socr/uploads/math/2/5/b/25bc401c8e13a8ce6ddff1b13a6d38f5.png) .
.
- standard deviation of X,
![SD[X]=\sqrt{\sum_{i=1}^k{(x_i-E[X])^2\times p_i}}](/socr/uploads/math/e/c/1/ec1ab41ffd1572663ead4c57dd736690.png) .
.
Synergies between Binomial and Multinomial processes/probabilities/coefficients
- The Binomial vs. Multinomial Coefficients
- The Binomial vs. Multinomial Formulas
- The Binomial vs. Multinomial Probabilities
Binomial Random Variables
Suppose we conduct an experiment observing an n-trial (fixed) Bernoulli process. If we are interested in the RV X={Number of successes in the n trials}, then X is called a Binomial RV and its distribution is called Binomial Distribution.
Examples
- Roll a standard die ten times. Let X be the number of times {6} turned up. The distribution of the random variable X is a binomial distribution with n = 10 (number of trials) and p = 1/6 (probability of "success={6}). The distribution of X may be explicitly written as (P(X=x) are rounded of, you can compute these exactly by going to SOCR Distributions and selecting Binomial):
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P(X=x) | 0.162 | 0.323 | 0.291 | 0.155 | 0.0543 | 0.013 | 0.0022 | 0.00025 | 0.000019 | 8.269e-7 | 1.654e-8 |
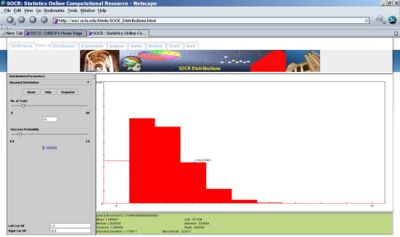
- Suppose 10% of the human population carries the green-eye allele. If we choose 1,000 people randomly and let the RV X be the number of green-eyed people in the sample. Then the distribution of X is binomial distribution with n = 1,000 and p = 0.1 (denoted as
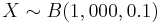 . In a sample of 1,000, how many are we expecting to have this allele?
. In a sample of 1,000, how many are we expecting to have this allele?
Binomial Modeling
Exact Binomial Model
The Binomial distribution (i.e., biased-coin tossing experiment) is an exact physical model for any experiment which can be characterized as a series of trials where:
- Each trial has only two outcomes: success or failure;
- P(success)=p is the same for every trial; and
- Trials are independent.
Approximate Binomial Model
Suppose we observe an experiment comprised of n identical trials involving a large population (of size N). Assume the population contains a sub-population of subjects that have a characteristic of interest and the sub-population proportion is p (0<p<1). Then the distribution of X={the number of outcomes in the sample with that characteristic of interest}, is approximately Binomial(n, p). This approximation is adequate if the ratio n/N < 0.05.
- Example: Polling the US population to see what proportion is/has-been married. Because we sample without replacement (can't ask the same individual twice), the second assumption of the (exact) Binomial model is (slightly) violated. Yet, the small ration of sample to population size yields that the Binomial model is approximately valid (i.e., the proportion of subjects that is/has-been married does not change significantly as we poll one subject, and therefore remove him/her from the complete pool of subjects we poll).
Binomial Probabilities
If the random variable X follows the Binomial distribution with (fixed) parameters n (sample-size) and p (probability of success at one trial), we write X ~ B(n, p). The probability of getting exactly x successes is given by the Binomial probability (or mass) function: 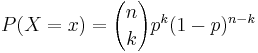 , for x = 0, 1, 2, ..., n, where
, for x = 0, 1, 2, ..., n, where 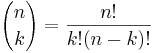 is the binomial coefficient.
is the binomial coefficient.
This probability expression has an easy and intuitive interpretation. The probability of the x successes in the n trials is (px). Similarly, the probability of the n-x failures is (1 − p)n-x. However, the x successes can be arranged anywhere among the n trials, and there are 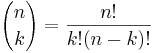 different ways of arranging the x successes in a sequence of n trials, see the Counting section.
different ways of arranging the x successes in a sequence of n trials, see the Counting section.
Binomial Expectation and Variance
If X is the random variable representing the r(random) number of heads in n coin toss trials, where the P(Head) = p, i.e., 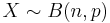 . Then we have the following expressions for the expected value, variance and the standard deviation of X :
. Then we have the following expressions for the expected value, variance and the standard deviation of X :
- Mean (expected value):
![E[X] = n\times p](/socr/uploads/math/2/d/a/2da32978a51032fb98cf78e07c923210.png) ,
,
- Variance:
![VAR[X] = n\times p \times(1-p)](/socr/uploads/math/4/3/9/4396f75ab09ef9e386d7c2418eae9184.png) , and
, and
- Standard deviation:
![SD[X] = \sqrt{n\times p \times(1-p)}](/socr/uploads/math/4/8/5/48548fd4bf6fa0c401a409af28d729f5.png)
- The complete description of the Binomial distribution is available here
Examples
Binomial Coin Toss Example
Refer to the SOCR Binomial Coin Toss Experiment and use the SOCR Binomial Coin Toss Applet to perform an experiment of tossing a biased coin, P(Head) = 0.3, 5 times and computing the expectation of the number of Heads in such experiment. You should recognize that there are two distinct ways of computing the expected number of Heads:
- Theoretical calculation, using the Binomial Probabilities;
E[X] = ∑ xP(X = x) = x
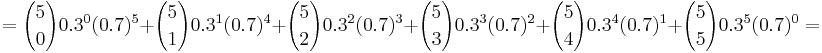
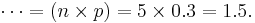
- Empirical calculation, using the outcomes 100 repeated coin tosses of 5 coins. The image below illustrates this approximate calculation of the expectation for the number of heads when
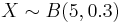 . Notice the slight difference between the theoretical expectation (
. Notice the slight difference between the theoretical expectation (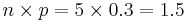 ) and its empirical approximation of 1.39!
) and its empirical approximation of 1.39!
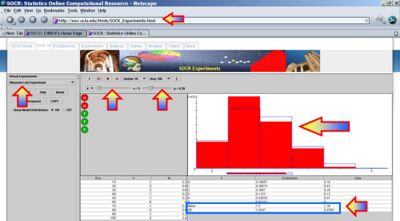
- Notes: Of course, the theoretical calculation is exact and the empirical calculation is only approximate. However, the power of the empirical approximation to the expected number of Heads becomes clear when we increase the number of coins from 5 to 100, or more. In these cases, the exact calculations become very difficult, and for even larger number of coins become intractable.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: