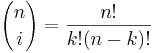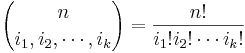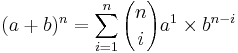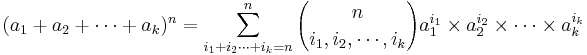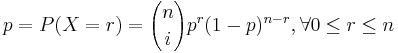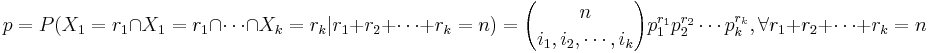AP Statistics Curriculum 2007 Distrib Multinomial
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Multinomial Random Variables and Experiments
The multinomial experiments (and multinomial distribtuions) directly extend the their bi-nomial counterparts.
- Examples of Multinomial experiments
- Rolling a hexagonal Die 5 times: Where the outcome space is the colection of 5-tuples, where each element is a value such that:
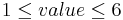 .
.
- Rolling a hexagonal Die 5 times: Where the outcome space is the colection of 5-tuples, where each element is a value such that:
- The Multinomial random variable (RV): Mathematically, a (k) multinomial trial is modeled by a random variable
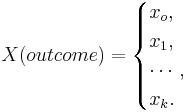
If pi = P(X = xi), then:
- expected value of X,
![E[X]=\sum_{i=1}^k{x_i\times p_i}](/socr/uploads/math/2/5/b/25bc401c8e13a8ce6ddff1b13a6d38f5.png) .
.
- standard deviation of X,
![SD[X]=\sqrt{\sum_{i=1}^k{(x_i-E[X])^2\times p_i}}](/socr/uploads/math/e/c/1/ec1ab41ffd1572663ead4c57dd736690.png) .
.
Synergies between Binomial and Multinomial processes/probabilities/coefficients
- The Binomial vs. Multinomial Coefficients
- The Binomial vs. Multinomial Formulas
- The Binomial vs. Multinomial Probabilities
Example
Suppose we study N independent trials with results falling in one of k possible categories labeled 1,2,cdots,k. Let pi be the probability of a trial resulting in the ith category, where  . Let Ni be the number of trials resulting in the ith category, where
. Let Ni be the number of trials resulting in the ith category, where  .
.
For instance, suppose we have 9 people arriving at a meeting according to the following information:
- P(by Air) = 0.4, P(by Bus) = 0.2, P(by Automobile) = 0.3, P(by Train) = 0.1
- Compute the following probabilities
- P(3 by Air, 3 by Bus, 1 by Auto, 2 by Train) = ?
- P(2 by air) = ?
SOCR Multinomial Examples
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: