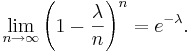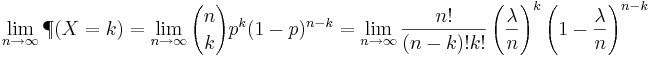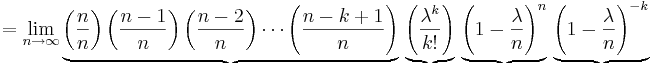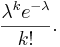AP Statistics Curriculum 2007 Distrib Poisson
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Poisson Random Variables and Experiments
Poisson Random Variables and Experiments
- Definition: Poisson Distribution is a discrete probability distribution that expresses the probability of the number of events occurring in a fixed period of time. These events occur with a known average rate and are independent of the time since the last event. The Poisson Distribution can also be used for the number of events in other specified intervals such as distance, area or volume.
- Mass function: For X~Poisson(λ), the Poisson mass function is given by
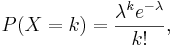 where
where
- e is the natural number (e = 2.71828...)
- k is the number of occurrences of an event - the probability of which is given by the mass function
-
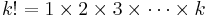
- λ is a positive real number, equal to the expected number of occurrences that occur during the given interval. For instance, if the events occur on average every 4 minutes, and you are interested in the number of events occurring in a 10 minute interval, you would use as model a Poisson distribution with λ=10/4=2.5.
- Notes
- The Poisson Distribution can be derived as a limiting case of the Binomial Distribution.
- The Poisson Distribution can be applied to systems with a large number of possible events, each of which is rare. A classic example is the nuclear decay of atoms and Positron Emission Tomography Imaging.
- Expectation: The expected value of a Poisson distributed random variable X is λ.
- Variance: The Poisson variance is λ.
- Example: See this SOCR Poisson distribution activity.
Example
Suppose one expects to see 40 shooting stars per hour at night (by observing at a specific location and not using visual enhancers). Assume that the process of observing arrivals (shooting stars) is Poisson(λ = 40).
- Compute the probability that in a 1 hour timeframe, the number of observed shooting stars will be between 44 and 52! We can compute this as follows: Let
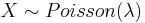 .
.
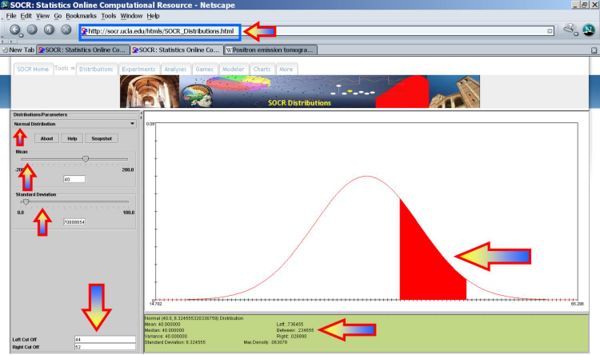
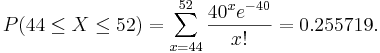 The figure below shows this result using SOCR distributions:
The figure below shows this result using SOCR distributions:
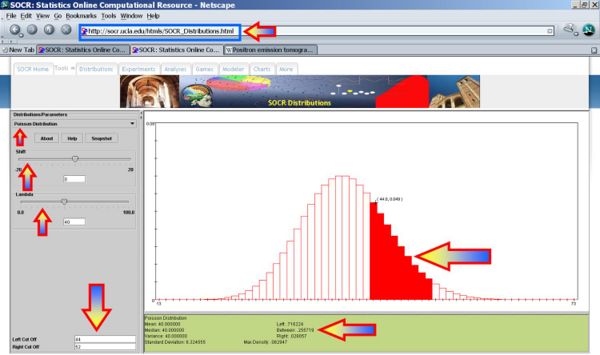
- Note: We observe that this distribution is bell-shaped. We can also use the Normal distribution to approximate this probability. Using
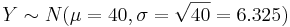 , together with the continuity correction for better approximation we obtain
, together with the continuity correction for better approximation we obtain 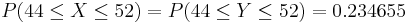 , which is close to the exact that was found earlier. The figure below shows this probability.
, which is close to the exact that was found earlier. The figure below shows this probability.
Applications
The Poisson Distribution arises in many different discrete situations when the probability of the observed phenomenon is constant in time or space. Examples of events that may be modeled by Poisson Distribution include:
- The number of cars that pass through a certain point on a road (sufficiently distant from traffic lights) during a given period of time.
- The number of spelling mistakes one makes while typing a single page.
- The number of phone calls at a call center per minute.
- The number of times a web server is accessed per minute.
- The number of road kill (animals killed) found per unit length of road.
- The number of mutations in a given stretch of DNA after a certain amount of radiation exposure.
- The number of unstable atomic nuclei that decayed within a given period of time in a piece of radioactive substance.
- The number of pine trees per unit area of mixed forest.
- The number of stars in a given volume of space.
- The distribution of visual receptor cells in the retina of the human eye.
- The number of light bulbs that burn out in a certain amount of time.
- The number of viruses that can infect a cell in cell culture.
- The number of hematopoietic stem cells in a sample of unfractionated bone marrow cells.
- The number of inventions of an inventor over their career.
- The number of particles that "scatter" off of a target in a nuclear or high energy physics experiment.
Poisson as a Limiting Case of Binomial Distribution
In several of the above examples, the events being counted are actually the outcomes of discrete trials, and would more precisely be modeled using the Binomial Distribution. However, the Binomial Distribution with parameters n (number of trials) and 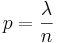 (probability of success). That is, Binomial approaches the Poisson distribution with expected value
(probability of success). That is, Binomial approaches the Poisson distribution with expected value 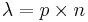 , as n approaches infinity. It provides a means to approximate Binomial random variables (for large n) using the Poisson distribution. The details of this approximation are below:
, as n approaches infinity. It provides a means to approximate Binomial random variables (for large n) using the Poisson distribution. The details of this approximation are below:
Let p = λ/n and 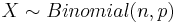 . Then we have
. Then we have
- As n approaches ∞, the first term approaches 1; the second remains constant since "n" does not appear in it at all; the third approaches e-λ; and the fourth expression approaches 1.
- Consequently the limit is
- More generally, whenever a sequence of binomial random variables with parameters n and pn is such that
the sequence convergence (in distribution) to a Poisson random variable with mean λ.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: