AP Statistics Curriculum 2007 EDA Freq
From Socr
(Difference between revisions)
ChiccoChou (Talk | contribs) (→Definitions) |
(→Definitions) |
||
| Line 6: | Line 6: | ||
===Definitions=== | ===Definitions=== | ||
* A '''frequency distribution''' is a display of the number (frequency) of occurrences of each value in a data set. | * A '''frequency distribution''' is a display of the number (frequency) of occurrences of each value in a data set. | ||
| - | * A '''relative frequency''' distribution is a display of the | + | * A '''relative frequency''' distribution is a display of the percentage (ratio or frequency to sample-size) of occurrences of each value in a data set. |
* A [http://en.wikipedia.org/wiki/Percentile percentile] is the <u>value</u> of a variable that divides the real line into two segments - the left one containing certain percent (say 13%) of the observations for the specific process, and the right interval containing the complementary percentage of observations (in this case 87%). The 30<sup>th</sup> percentile is the value (measurement) bound above 30% and below 70% of the observations from a process. | * A [http://en.wikipedia.org/wiki/Percentile percentile] is the <u>value</u> of a variable that divides the real line into two segments - the left one containing certain percent (say 13%) of the observations for the specific process, and the right interval containing the complementary percentage of observations (in this case 87%). The 30<sup>th</sup> percentile is the value (measurement) bound above 30% and below 70% of the observations from a process. | ||
* The (three) '''quartiles''' are the special cases of percentiles for Q<sub>1</sub>=25%, Q<sub>2</sub>=50% (median) and Q<sub>3</sub>=75%. | * The (three) '''quartiles''' are the special cases of percentiles for Q<sub>1</sub>=25%, Q<sub>2</sub>=50% (median) and Q<sub>3</sub>=75%. | ||
Revision as of 21:01, 4 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Summarizing data with Frequency Tables
Summarizing data with Frequency Tables & Histograms
There are two ways to describe a data set (sample from a population) - Pictorial Graphs or Tables of Numbers. Both are important for analyzing data.
Definitions
- A frequency distribution is a display of the number (frequency) of occurrences of each value in a data set.
- A relative frequency distribution is a display of the percentage (ratio or frequency to sample-size) of occurrences of each value in a data set.
- A percentile is the value of a variable that divides the real line into two segments - the left one containing certain percent (say 13%) of the observations for the specific process, and the right interval containing the complementary percentage of observations (in this case 87%). The 30th percentile is the value (measurement) bound above 30% and below 70% of the observations from a process.
- The (three) quartiles are the special cases of percentiles for Q1=25%, Q2=50% (median) and Q3=75%.
Example
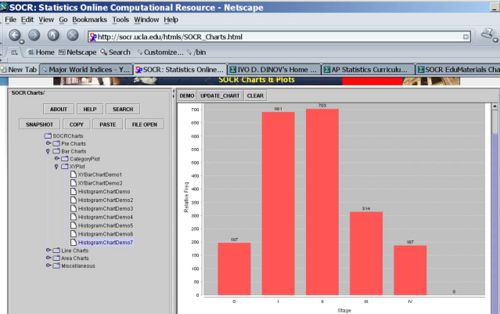
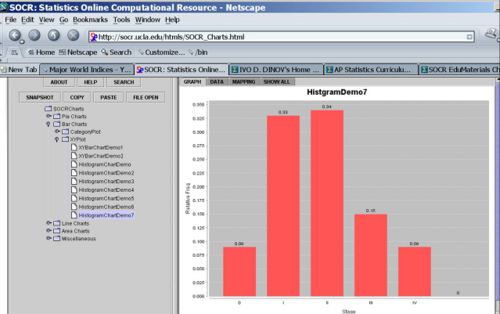
The table below shows the stage of disease at diagnosis of breast cancer in a random sample of 2092 US women.
| Stage | Frequency | Relative Frequency |
|---|---|---|
| 0 | 197 | 0.09 |
| I | 691 | 0.33 |
| II | 703 | 0.34 |
| III | 314 | 0.15 |
| IV | 187 | 0.09 |
| Total | 2092 | 1.00 |
Computational Resources: Internet-based SOCR Tools
- SOCR Charts allows you to generate graphical representations (including frequency histograms) of a variety of datasets.
- The SOCR Charts activities provide usage-instructions, examples and demonstrations of how to use SOCR Charts.
Hands-on activities
You can copy and paste the first 2 columns in the data table above in the SOCR Charts (BarChart --> XYPlot --> HistogramDemo7). You can see this SOCR Charts activity for help with histogram plots.
- The graph below illustrates the (raw) frequency histogram (using counts)
- The graph below show the relative frequency histogram (using the last column of the table above).
Problems
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
