AP Statistics Curriculum 2007 EDA Shape
From Socr
(Difference between revisions)
(→Definitions) |
|||
| (8 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Measures of Shape== | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Measures of Shape== | ||
| - | === | + | ===Definitions=== |
| - | + | * A distribution is '''unimodal''' if it has one mode. Unimodal distributions include: | |
| - | + | ** Bell shaped distributions (symmetric, Normal) | |
| + | ** Skewed right or skewed left | ||
| + | ** We can use the [[AP_Statistics_Curriculum_2007_EDA_Center | mean and median]] to help interpret the shape of a distribution. For an unimodal distribution we have these properties: | ||
| + | *** If '''mean = median''', then the distribution is symmetric | ||
| + | *** If '''mean > median''', then the distribution is right skewed | ||
| + | *** If '''mean < median''', then the distribution is left skewed | ||
| - | + | * '''Multimodal''' distributions have two or more modes. Examples of multimodal distributions are: | |
| - | + | ** [http://en.wikipedia.org/wiki/U-quadratic_distribution U Quadratic] | |
| + | ** [[SOCR_EduMaterials_ModelerActivities_MixtureModel_1 | Mixture Distributions]] | ||
| + | <center>[[Image:SOCR_EBook_Dinov_EDA_012708_Fig9.jpg|500px]]</center> | ||
| - | + | ===Other Measures of Shape=== | |
| - | + | [[AP_Statistics_Curriculum_2007_Distrib_MeanVar | This section also provides moment-based characterization of distribution shape]]. | |
| - | === | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
===Examples=== | ===Examples=== | ||
| - | + | What seems like a logical choice for the shape of [[AP_Statistics_Curriculum_2007_EDA_Pics#Example | the hot dog calorie data]]? Try looking at the histogram of the calories for the [[SOCR_012708_ID_Data_HotDogs |Hot-dogs dataset]]. | |
| + | <center>[[Image:SOCR_EBook_Dinov_EDA_012708_Fig4.jpg|500px]]</center> | ||
| - | * | + | ===Activities=== |
| + | Collect data, draw the sample histogram or dot-plot and classify the shape of the distribution accordingly. Also, if unimodal, classify symmetry (symmetric, skewed right or skewed left). | ||
| + | *Data collected on height of randomly sampled college students. | ||
| + | *Data collected on height of randomly sampled female college students. | ||
| + | *The salaries of all persons employed by a large university. | ||
| + | *The amount of time spent by students on a difficult exam. | ||
| + | *The grade distribution on a difficult exam. | ||
===Hands-on activities=== | ===Hands-on activities=== | ||
| - | + | * [[SOCR_EduMaterials_Activities_RNG | You can generate data using the SOCR Modeler as shown here]]. | |
| - | + | * [[SOCR_EduMaterials_ModelerActivities_MixtureModel_1 | Try fitting multi-model mixture models to samples of 2 Normal distributions with very different centers]] | |
| - | * | + | |
| - | + | ===[[EBook_Problems_EDA_Shape | Problems]]=== | |
| - | === | + | |
| - | + | ||
<hr> | <hr> | ||
Current revision as of 21:08, 4 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Measures of Shape
Definitions
- A distribution is unimodal if it has one mode. Unimodal distributions include:
- Bell shaped distributions (symmetric, Normal)
- Skewed right or skewed left
- We can use the mean and median to help interpret the shape of a distribution. For an unimodal distribution we have these properties:
- If mean = median, then the distribution is symmetric
- If mean > median, then the distribution is right skewed
- If mean < median, then the distribution is left skewed
- Multimodal distributions have two or more modes. Examples of multimodal distributions are:
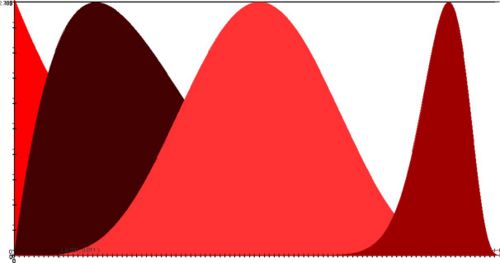
Other Measures of Shape
This section also provides moment-based characterization of distribution shape.
Examples
What seems like a logical choice for the shape of the hot dog calorie data? Try looking at the histogram of the calories for the Hot-dogs dataset.
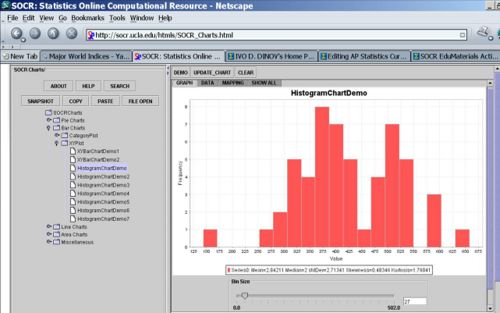
Activities
Collect data, draw the sample histogram or dot-plot and classify the shape of the distribution accordingly. Also, if unimodal, classify symmetry (symmetric, skewed right or skewed left).
- Data collected on height of randomly sampled college students.
- Data collected on height of randomly sampled female college students.
- The salaries of all persons employed by a large university.
- The amount of time spent by students on a difficult exam.
- The grade distribution on a difficult exam.
Hands-on activities
- You can generate data using the SOCR Modeler as shown here.
- Try fitting multi-model mixture models to samples of 2 Normal distributions with very different centers
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
