AP Statistics Curriculum 2007 EDA Shape
From Socr
(Difference between revisions)
(→Definitions) |
|||
| (3 intermediate revisions not shown) | |||
| Line 5: | Line 5: | ||
** Bell shaped distributions (symmetric, Normal) | ** Bell shaped distributions (symmetric, Normal) | ||
** Skewed right or skewed left | ** Skewed right or skewed left | ||
| - | ** We can use the [[AP_Statistics_Curriculum_2007_EDA_Center | mean and median]] to help interpret the shape of a distribution. For | + | ** We can use the [[AP_Statistics_Curriculum_2007_EDA_Center | mean and median]] to help interpret the shape of a distribution. For an unimodal distribution we have these properties: |
*** If '''mean = median''', then the distribution is symmetric | *** If '''mean = median''', then the distribution is symmetric | ||
*** If '''mean > median''', then the distribution is right skewed | *** If '''mean > median''', then the distribution is right skewed | ||
*** If '''mean < median''', then the distribution is left skewed | *** If '''mean < median''', then the distribution is left skewed | ||
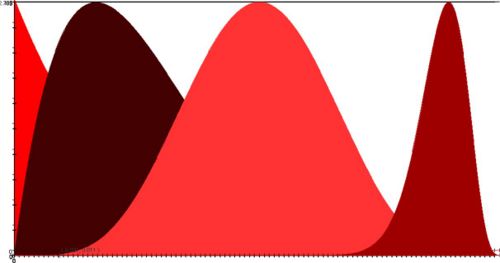
| - | * '''Multimodal''' distributions have two or more | + | * '''Multimodal''' distributions have two or more modes. Examples of multimodal distributions are: |
** [http://en.wikipedia.org/wiki/U-quadratic_distribution U Quadratic] | ** [http://en.wikipedia.org/wiki/U-quadratic_distribution U Quadratic] | ||
** [[SOCR_EduMaterials_ModelerActivities_MixtureModel_1 | Mixture Distributions]] | ** [[SOCR_EduMaterials_ModelerActivities_MixtureModel_1 | Mixture Distributions]] | ||
<center>[[Image:SOCR_EBook_Dinov_EDA_012708_Fig9.jpg|500px]]</center> | <center>[[Image:SOCR_EBook_Dinov_EDA_012708_Fig9.jpg|500px]]</center> | ||
| + | |||
| + | ===Other Measures of Shape=== | ||
| + | [[AP_Statistics_Curriculum_2007_Distrib_MeanVar | This section also provides moment-based characterization of distribution shape]]. | ||
===Examples=== | ===Examples=== | ||
| Line 30: | Line 33: | ||
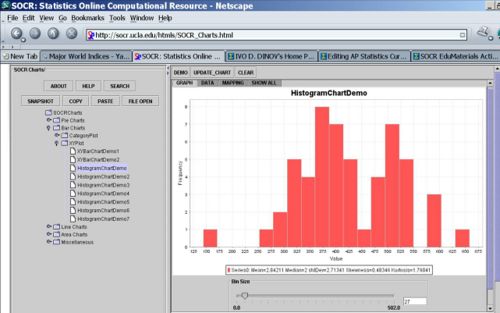
* [[SOCR_EduMaterials_Activities_RNG | You can generate data using the SOCR Modeler as shown here]]. | * [[SOCR_EduMaterials_Activities_RNG | You can generate data using the SOCR Modeler as shown here]]. | ||
* [[SOCR_EduMaterials_ModelerActivities_MixtureModel_1 | Try fitting multi-model mixture models to samples of 2 Normal distributions with very different centers]] | * [[SOCR_EduMaterials_ModelerActivities_MixtureModel_1 | Try fitting multi-model mixture models to samples of 2 Normal distributions with very different centers]] | ||
| + | |||
| + | ===[[EBook_Problems_EDA_Shape | Problems]]=== | ||
<hr> | <hr> | ||
Current revision as of 21:08, 4 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Measures of Shape
Definitions
- A distribution is unimodal if it has one mode. Unimodal distributions include:
- Bell shaped distributions (symmetric, Normal)
- Skewed right or skewed left
- We can use the mean and median to help interpret the shape of a distribution. For an unimodal distribution we have these properties:
- If mean = median, then the distribution is symmetric
- If mean > median, then the distribution is right skewed
- If mean < median, then the distribution is left skewed
- Multimodal distributions have two or more modes. Examples of multimodal distributions are:
Other Measures of Shape
This section also provides moment-based characterization of distribution shape.
Examples
What seems like a logical choice for the shape of the hot dog calorie data? Try looking at the histogram of the calories for the Hot-dogs dataset.
Activities
Collect data, draw the sample histogram or dot-plot and classify the shape of the distribution accordingly. Also, if unimodal, classify symmetry (symmetric, skewed right or skewed left).
- Data collected on height of randomly sampled college students.
- Data collected on height of randomly sampled female college students.
- The salaries of all persons employed by a large university.
- The amount of time spent by students on a difficult exam.
- The grade distribution on a difficult exam.
Hands-on activities
- You can generate data using the SOCR Modeler as shown here.
- Try fitting multi-model mixture models to samples of 2 Normal distributions with very different centers
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
