AP Statistics Curriculum 2007 EDA Var
From Socr
| Line 14: | Line 14: | ||
===Range=== | ===Range=== | ||
The range is the easiest measure of dispersion to calculate, yet, perhaps not the best measure. The '''Range = max - min'''. For example, for the Long Jump data, the range is calculated by: | The range is the easiest measure of dispersion to calculate, yet, perhaps not the best measure. The '''Range = max - min'''. For example, for the Long Jump data, the range is calculated by: | ||
| - | <center | + | <center>Range = 106 – 60 = 46.</center> |
| + | |||
| + | Note that the range is only sensitive to the extreme values of a sample and ignores all other information. So, two completely different distributions may have the same range. | ||
===Variance and Standard Deviation=== | ===Variance and Standard Deviation=== | ||
| - | The logic behind the variance and standard deviation measures is to measure the difference between each observation and the mean (i.e., dispersion). The deviation of the i | + | The logic behind the variance and standard deviation measures is to measure the difference between each observation and the mean (i.e., dispersion). Suppose we have ''n > 1'' observations, <math>\left \{ y_1, y_2, y_3, ..., y_n \right \}</math>. The deviation of the <math>i^{th}</math> measurement, <math>y_i</math>, from the mean (<math>\overline{y}</math>) is defined by <math>(y_i - \overline{y})</math>. |
Does the average of these deviations seem like a reasonable way to find an average deviation for the sample or the population? No, because the sum of all deviations is trivial: | Does the average of these deviations seem like a reasonable way to find an average deviation for the sample or the population? No, because the sum of all deviations is trivial: | ||
| Line 23: | Line 25: | ||
To solve this problem we employ different versions of the '''mean absolute deviation''': | To solve this problem we employ different versions of the '''mean absolute deviation''': | ||
| - | <center><math>\sum_{i=1}^n{|y_i - \overline{y}|}.</math></center> | + | <center><math>{1 \over n-1}\sum_{i=1}^n{|y_i - \overline{y}|}.</math></center> |
In particular, the '''variance''' is defined as: | In particular, the '''variance''' is defined as: | ||
| - | <center><math>\sum_{i=1}^n{|y_i - \overline{y}|^2}.</math></center> | + | <center><math>{1 \over n-1}\sum_{i=1}^n{|y_i - \overline{y}|^2}.</math></center> |
And the '''standard deviation''' is defined as: | And the '''standard deviation''' is defined as: | ||
| - | <center><math>\sqrt{\sum_{i=1}^n{|y_i - \overline{y}|^2}}.</math></center> | + | <center><math>\sqrt{{1 \over n-1}\sum_{i=1}^n{|y_i - \overline{y}|^2}}.</math></center> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Some software packages may use <math>{1 \over n}</math>, instead of the <math>{1 \over n-1}</math>, which we used above. Note that for large sample-sizes this difference becomes increasingly smaller. Also, there are theoretical properties of the sample variance, as defined above (e.g., sample-variance is an unbiased estimate of the population-variance!) | |
| - | + | Most of the [http://socr.ucla.edu/htmls/SOCR_Charts.html SOCR Charts] and http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] compute the variance or standard deviation for the sample. You can see these examples of [[SOCR_EduMaterials_ChartsActivities | Charts Activities]] and [[SOCR_EduMaterials_AnalysesActivities | Analyses Activities]] and you can test these using [[SOCR_012708_ID_Data_HotDogs | hotdogs dataset]]. | |
| - | + | ||
| - | |||
<hr> | <hr> | ||
Revision as of 03:37, 28 January 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Measures of Variation
Measures of Variation and Dispersion
There are many measures of (population or sample) variation, e.g., the range, the variance, the standard deviation, mean absolute deviation, etc. These are used to assess the dispersion or spread of the population.
Suppose we are interested in the long-jump performance of some students. We can carry an experiment by randomly selecting 8 male statistics students and ask them to perform the standing long jump. In reality every student participated, but for the ease of calculations below we will focus on these eight students. The long jumps were as follows:
| 74 | 78 | 106 | 80 | 68 | 64 | 60 | 76 |
Range
The range is the easiest measure of dispersion to calculate, yet, perhaps not the best measure. The Range = max - min. For example, for the Long Jump data, the range is calculated by:
Note that the range is only sensitive to the extreme values of a sample and ignores all other information. So, two completely different distributions may have the same range.
Variance and Standard Deviation
The logic behind the variance and standard deviation measures is to measure the difference between each observation and the mean (i.e., dispersion). Suppose we have n > 1 observations, 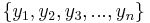 . The deviation of the ith measurement, yi, from the mean (
. The deviation of the ith measurement, yi, from the mean ( ) is defined by
) is defined by  .
.
Does the average of these deviations seem like a reasonable way to find an average deviation for the sample or the population? No, because the sum of all deviations is trivial:
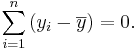
To solve this problem we employ different versions of the mean absolute deviation:
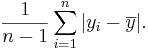
In particular, the variance is defined as:
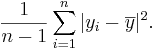
And the standard deviation is defined as:
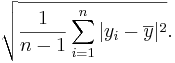
Some software packages may use 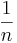 , instead of the
, instead of the 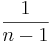 , which we used above. Note that for large sample-sizes this difference becomes increasingly smaller. Also, there are theoretical properties of the sample variance, as defined above (e.g., sample-variance is an unbiased estimate of the population-variance!)
, which we used above. Note that for large sample-sizes this difference becomes increasingly smaller. Also, there are theoretical properties of the sample variance, as defined above (e.g., sample-variance is an unbiased estimate of the population-variance!)
Most of the SOCR Charts and http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses] compute the variance or standard deviation for the sample. You can see these examples of Charts Activities and Analyses Activities and you can test these using hotdogs dataset.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
