AP Statistics Curriculum 2007 Estim L Mean
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Estimating a Population Mean: Large Samples
This section discusses how to find point and interval estimates when the sample-sizes are large. For most applications, sample-sizes exceeding 100 may be considered as large. However, in practice even samples larger than 30 may be considered large. Yet, sometimes, samples must be > 1,000, or even 100,000 to be considered large. The next section presents the estimation for small-samples.
Point Estimation of a Population Mean
For any process, the population mean may be estimated by a (large) sample average. That is the sample average 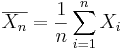 , constructed from a random sample of the procees {
, constructed from a random sample of the procees {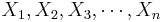 }, is an unbiased estimate of the population mean μ, if it exists! Note that the sample average may be susceptible to outliers.
}, is an unbiased estimate of the population mean μ, if it exists! Note that the sample average may be susceptible to outliers.
Interval Estimation of a Population Mean
For large samples, interval estimation of the population means (or Confidence intervals) are constructed as follows. Choose a confidence level (1 − α)100%, where α is small (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.). Then a (1 − α)100% confidence interval for μ will be
- The margin of error E is defined as

- The Standard Error of the estimate
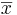 is obtained by replacing the unknown population standard deviation by the sample standard deviation:
is obtained by replacing the unknown population standard deviation by the sample standard deviation:
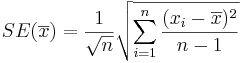
-
 is the critical value for a Standard Normal distribution at
is the critical value for a Standard Normal distribution at 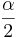 .
.
Example
Market researchers use the number of sentences per advertisement as a measure of readability for magazine advertisements. A random sample of the number of sentences found in 30 magazine advertisements is listed. Use this sample to find point estimate for the population mean μ.
| 16 | 9 | 14 | 11 | 17 | 12 | 99 | 18 | 13 | 12 | 5 | 9 | 17 | 6 | 11 | 17 | 18 | 20 | 6 | 14 | 7 | 11 | 12 | 5 | 18 | 6 | 4 | 13 | 11 | 12 |
A confidence interval estimate of μ is a range of values used to estimate a population parameter (interval estimates are normally used more than point estimates because it is very unlikely that the sample mean would match exactly with the population mean) The interval estimate uses a margin of error about the point estimate. For example if you have a point estimate of 12. 25 with a margin of error of 1.75, then the interval estimate would be (10.5 to 14).
Before you find an interval estimate, you should first determine how confident you want to be that your interval estimate contains the population mean.
- 80% confidence (0.80), α = 0.1, z = 1.28
- 90% confidence (0.90), α = 0.05, z = 1.645
- 95% confidence (0.95), α = 0.025, z = 1.96
- 99% confidence (0.99), α = 0.005, z = 2.575
Known Variance
Suppose that we know the variance for the number of sentences per advertisement example above is known to be 256 (so the population standard deviation is σ = 16).
- For α = 0.1, the 80%CI(μ) is constructed by:
![\overline{x}\pm 1.28{16\over \sqrt{30}}=14.77 \pm 1.28{16\over \sqrt{30}}=[11.03;18.51]](/socr/uploads/math/6/6/8/66888e34b899051240c1c64526de2688.png)
- For α = 0.05, the 90%CI(μ) is constructed by:
![\overline{x}\pm 1.645{16\over \sqrt{30}}=14.77 \pm 1.645{16\over \sqrt{30}}=[9.96;19.57]](/socr/uploads/math/b/0/4/b047fdaa02a2672084c34c7771d6695f.png)
- For α = 0.005, the 99%CI(μ) is constructed by:
![\overline{x}\pm 2.575{16\over \sqrt{30}}=14.77 \pm 2.575{16\over \sqrt{30}}=[7.24;22.29]](/socr/uploads/math/b/9/a/b9a18b5bd93301e588b3ca25de03d629.png)
Notice the increase of the CI's (directly related to the decrease of α) reflecting our choice for higher confidence.
Unknown variance
Suppose that we do not know the variance for the number of sentences per advertisement but use the sample variance 273 as an estimate (so the sample standard deviation is 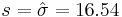 ).
).
- For α = 0.1, the 90%CI(μ) is constructed by:
![\overline{x}\pm 1.28{16\over \sqrt{30}}=14.77 \pm 1.28{16.54\over \sqrt{30}}=[10.90;18.63]](/socr/uploads/math/b/2/5/b25bd21de38eeebf5ce2bab05914a5f7.png)
- For α = 0.05, the 90%CI(μ) is constructed by:
![\overline{x}\pm 1.645{16\over \sqrt{30}}=14.77 \pm 1.645{16.54\over \sqrt{30}}=[9.80;19.73]](/socr/uploads/math/5/5/2/55266505899de49ebcc6ea22908661ca.png)
- For α = 0.005, the 90%CI(μ) is constructed by:
![\overline{x}\pm 2.575{16\over \sqrt{30}}=14.77 \pm 2.575{16.54\over \sqrt{30}}=[6.99;22.54]](/socr/uploads/math/d/0/b/d0bf8a8dfcc01008e2a2ded4b902d248.png)
Notice the increase of the CI's (directly related to the decrease of α) reflecting our choice for higher confidence.
Hands-on activities
- See the SOCR Confidence Interval Experiment.
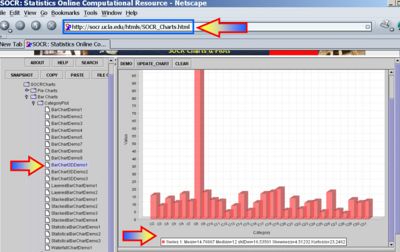
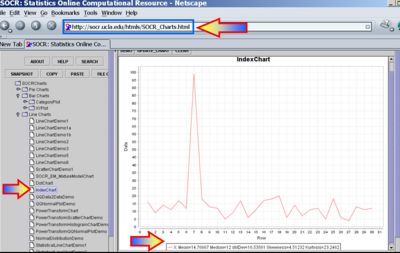
- Sample statistics, like the sample-mean and the sample-variance, may be easily obtained using SOCR Charts. The images below illustrate this functionality (based on the Bar-Chart and Index-Chart) using the 30 observations of the number of sentences per advertisement, reported above.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: