AP Statistics Curriculum 2007 Estim MOM MLE
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Method of Moments and Maximum Likelihood Estimation
Suppose we flip a coin 8 times and observe the number of heads (successes) in the outcomes. How would we estimate the true (unknown) probability of a Head (P(H)=?) for this specific coin? There are a number of other similar situations where we need to evaluate, predict or estimate a population (or process) parameter of interest using an observed data sample.
There are many ways to obtain point (value) estimates of various population parameters of interest, using observed data from the specific process we study. The method of moments and the maximum likelihood estimation are among the most popular ones frequently used in practice.
Method of Moments (MOM) Estimation
Parameter estimation using the method of moments is both intuitive and easy to calculate. The idea is to use the sample data to calculate some sample moments and then set these equal to their corresponding population counterparts. Typically the latter involve the parameter(s) that we are interested in estimating and thus we obtain a computationally tractable protocol for their estimation. Summarizing the MOM:
- First: Determine the k parameters of interest and the specific (model) distribution for this process;
- Second: Compute the first k (or more) sample-moments;
- Third: Set the sample-moments equal to the population moments and solve a (linear or non-linear) system of k equations with k unknowns.
MOM Proportion Example
Let's look at the motivational problem we discussed above. We want to flip a coin 8 times, observe the number of heads (successes) in the outcomes and use that to inffer the true (unknown) probability of a Head (P(H)=?) for this specific coin.
- Hypothetical solution: Suppose we observe the following sequence of outcomes {T,H,T,H,H,T,H,H}. Using the MOM protocol we obtain:
- There is one parameter of interest p=P(H) and the process is a Binomial experiment.
- The first sample-moment for a Binomial process is p=E(X). Therefore, if the random variable X = {# H’s}, then np=8p=E(X)= Sample#H’s = 5 , which yeields that the first sample moment is
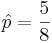 . Hence, we would estimate the uknown
. Hence, we would estimate the uknown 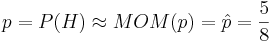 .
.
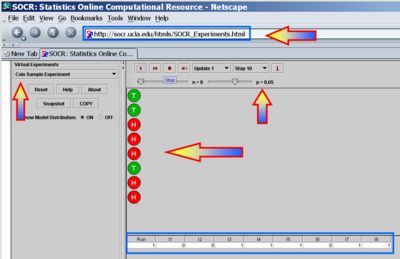
- Experimental Solution: We can also use SOCR Experiments to demonstrate the MOM estimation technique. You can refer to the SOCR Coin Sample Experiment for more information of this SOCR applet. The The figure below illustrates flipping a coin 8 times and observing 5 Heads. This is a Binomial(n=8, p=0.65) distribution. However, let's pretend for a minute that we did not know the actual p=P(H) value! So we have a good approximation
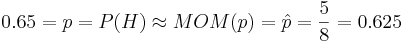 . Of course, if we run this experiment again, our MOM estimate for p would change!
. Of course, if we run this experiment again, our MOM estimate for p would change!
More information about the method of mements for parameter (point) estimation may be found here.
Maximum Likelihood Estimation (MLE)
Maximum likelihood estimation (MLE) is another popular statistical technique for parameter estimation. Modeling distribution parameters using MLE estimation based on observed real world data offers a way of tuning the free parameters of the model to provide an optimum fit.
Summarizing the MOM:
- First: Determine the k parameters of interest and the specific (model) distribution for this process;
- Second: Compute the first k (or more) sample-moments;
- Third: Set the sample-moments equal to the population moments and solve a (linear or non-linear) system of k equations with k unknowns.
MOM Proportion Example
Let's look at the motivational problem we discussed above. We want to flip a coin 8 times, observe the number of heads (successes) in the outcomes and use that to inffer the true (unknown) probability of a Head (P(H)=?) for this specific coin.
- Hypothetical solution: Suppose we observe the following sequence of outcomes {T,H,T,H,H,T,H,H}. Using the MOM protocol we obtain:
- There is one parameter of interest p=P(H) and the process is a Binomial experiment.
- The first sample-moment for a Binomial process is p=E(X). Therefore, if the random variable X = {# H’s}, then np=8p=E(X)= Sample#H’s = 5 , which yeields that the first sample moment is
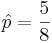 . Hence, we would estimate the uknown
. Hence, we would estimate the uknown 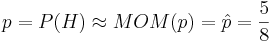 .
.
- Experimental Solution: We can also use SOCR Experiments to demonstrate the MOM estimation technique. You can refer to the SOCR Coin Sample Experiment for more information of this SOCR applet. The The figure below illustrates flipping a coin 8 times and observing 5 Heads. This is a Binomial(n=8, p=0.65) distribution. However, let's pretend for a minute that we did not know the actual p=P(H) value! So we have a good approximation
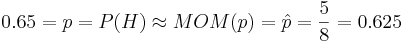 . Of course, if we run this experiment again, our MOM estimate for p would change!
. Of course, if we run this experiment again, our MOM estimate for p would change!
MOM vs. MLE
- The MOM is inferior to Fisher's MLE method, because maximum likelihood estimators have higher probability of being close to the quantities to be estimated.
- MLE may be intractable in some situations, whereas the MOM estimates can be quickly and easily calculated by hand or using a computer.
- MOM estimates may be used as the first approximations to the solutions of the MLE method, and successive improved approximations may then be found by the Newton-Raphson method. In this respect, the MOM and MLE are symbiotic.
- Sometimes, MOM estimates may be outside of the parameter space; i.e., they are unreliable, which is never a problem with the MLE method.
- MOM estimates are not necessarily sufficient statistics, i.e., they sometimes fail to take into account all relevant information in the sample.
- MOM may be prefered to MLE for estimating some structural parameters (e.g., parameters of a utility function, instead of parameters of a known probability distribution), when appropriate probability distributions are unknown.
Parameter Estimation Examples
The SOCR Modeler and the corresponfing SOCR Modeler Activities provide a number of interesting examples of parameter (point) estimation in terms of fitting best models to observed data.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
