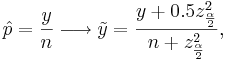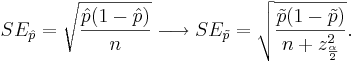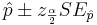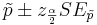AP Statistics Curriculum 2007 Estim Proportion
From Socr
(→Estimating a Population Proportion) |
|||
| Line 3: | Line 3: | ||
=== Estimating a Population Proportion=== | === Estimating a Population Proportion=== | ||
| - | When the sample size is large, the sampling distribution of the sample proportion <math>\hat{p}</math> is approximately Normal, by [[AP_Statistics_Curriculum_2007_Limits_CLT |CLT]], as the sample proportion may be presented as a [[AP_Statistics_Curriculum_2007_Limits_Norm2Bin |sample average or Bernoulli random variables]]. When the sample size is small, the normal approximation may be inadequate. To accommodate this we will modify <math>\hat{p}</math> slightly | + | When the sample size is large, the sampling distribution of the sample proportion <math>\hat{p}</math> is approximately Normal, by [[AP_Statistics_Curriculum_2007_Limits_CLT |CLT]], as the sample proportion may be presented as a [[AP_Statistics_Curriculum_2007_Limits_Norm2Bin |sample average or Bernoulli random variables]]. When the sample size is small, the normal approximation may be inadequate. To accommodate this we will modify the '''sample-proportion''' <math>\hat{p}</math> slightly and obtain the '''corrected-sample-proportion''' <math>\tilde{p}</math>: |
: <math>\hat{p}={y\over n} \longrightarrow \tilde{y}={y+0.5z_{\alpha \over 2}^2 \over n+z_{\alpha \over 2}^2},</math> | : <math>\hat{p}={y\over n} \longrightarrow \tilde{y}={y+0.5z_{\alpha \over 2}^2 \over n+z_{\alpha \over 2}^2},</math> | ||
where [[AP_Statistics_Curriculum_2007_Normal_Critical | <math>z_{\alpha \over 2}</math> is the normal critical value we saw earlier]]. | where [[AP_Statistics_Curriculum_2007_Normal_Critical | <math>z_{\alpha \over 2}</math> is the normal critical value we saw earlier]]. | ||
| Line 9: | Line 9: | ||
The standard error of <math>\hat{p}</math> also needs a slight modification | The standard error of <math>\hat{p}</math> also needs a slight modification | ||
: <math>SE_{\hat{p}} = \sqrt{\hat{p}(1-\hat{p})\over n} \longrightarrow SE_{\tilde{p}} = \sqrt{\tilde{p}(1-\tilde{p})\over n+z_{\alpha \over 2}^2}.</math> | : <math>SE_{\hat{p}} = \sqrt{\hat{p}(1-\hat{p})\over n} \longrightarrow SE_{\tilde{p}} = \sqrt{\tilde{p}(1-\tilde{p})\over n+z_{\alpha \over 2}^2}.</math> | ||
| - | |||
===Confidence intervals for proportions=== | ===Confidence intervals for proportions=== | ||
Revision as of 05:12, 4 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Estimating a Population Proportion
Estimating a Population Proportion
When the sample size is large, the sampling distribution of the sample proportion 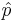 is approximately Normal, by CLT, as the sample proportion may be presented as a sample average or Bernoulli random variables. When the sample size is small, the normal approximation may be inadequate. To accommodate this we will modify the sample-proportion
is approximately Normal, by CLT, as the sample proportion may be presented as a sample average or Bernoulli random variables. When the sample size is small, the normal approximation may be inadequate. To accommodate this we will modify the sample-proportion 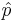 slightly and obtain the corrected-sample-proportion
slightly and obtain the corrected-sample-proportion 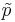 :
:
where  is the normal critical value we saw earlier.
is the normal critical value we saw earlier.
The standard error of 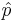 also needs a slight modification
also needs a slight modification
Confidence intervals for proportions
The confidence intervals for the sample proportion 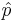 and the corrected-sample-proportion
and the corrected-sample-proportion 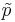 are given by
are given by
Model Validation
Checking/affirming underlying assumptions.
- TBD
Computational Resources: Internet-based SOCR Tools
- TBD
Examples
Computer simulations and real observed data.
- TBD
Hands-on activities
Step-by-step practice problems.
- TBD
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: