AP Statistics Curriculum 2007 Estim Proportion
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Estimating a Population Proportion
Estimating a Population Proportion
When the sample size is large, the sampling distribution of the sample proportion 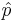 is approximately Normal, by CLT, as the sample proportion may be presented as a sample average or Bernoulli random variables. When the sample size is small, the normal approximation may be inadequate. To accommodate this we will modify the sample-proportion
is approximately Normal, by CLT, as the sample proportion may be presented as a sample average or Bernoulli random variables. When the sample size is small, the normal approximation may be inadequate. To accommodate this we will modify the sample-proportion 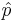 slightly and obtain the corrected-sample-proportion
slightly and obtain the corrected-sample-proportion 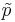 :
:
where  is the normal critical value we saw earlier.
is the normal critical value we saw earlier.
The standard error of 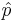 also needs a slight modification
also needs a slight modification
Confidence intervals for proportions
The confidence intervals for the sample proportion 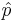 and the corrected-sample-proportion
and the corrected-sample-proportion 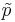 are given by
are given by
Example
Suppose a researcher is interested in studying the effect of aspirin in reducing heart attacks. He randomly recruits 500 subjects with evidence of early heart disease and has them take one aspirin daily for two years. At the end of the two years he finds that during the study only 17 subjects had a heart attack. Calculate a 95% (α = 0.05) confidence interval for the true (unknown) proportion of subjects with early heart disease that have a heart attack while taking aspirin daily. Note that 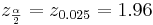 :
:
-
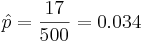 ;
; 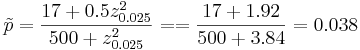
-
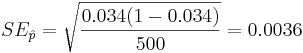 ;
; 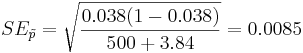
And the corresponding confidence intervals are given by
Sample-size estimation
For a given margin of error we can derive the minimum sample-size that guarantees an interval estimate within the given margin of error. The margin of error is the standard-error of the sample-proportion:
This equation has one unknown parameter (n), which we can solve for if we are given an upper limit for the margin of error.
- Failed to parse (syntax error): SE_{\tilde{p}} \geq \sqrt{\tilde{p}(1-\tilde{p})\over n+z_{\alpha \over 2}^2} \longrightarrow n \geq {\tilde{p}(1-\tilde{p})\over SE_{\tilde{p}^2} } -z_{\alpha \over 2}^2}.
Example
How many subjects are needed if the heart-researchers want SE < 0.005 for a 95% CI, and have a guess based on previous research that 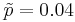 ?
?
- n \geq {0.04(1-0.04)\over 0.005^2} } - 1.96^2}=1533.16 \approx 1534.</math>
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
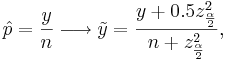
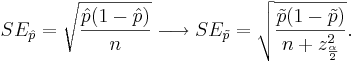
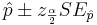
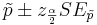
![\hat{p}\pm 1.96 SE_{\hat{p}}=[0.026944, 0.041056]](/socr/uploads/math/f/4/9/f49b24d961591662728fe7f3c783ffc9.png)
![\tilde{p}\pm 1.96 SE_{\tilde{p}}=[0.0213, 0.0547]](/socr/uploads/math/5/9/0/590c88e222c811d943bc36eeae550bd2.png)