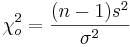AP Statistics Curriculum 2007 Estim Var
From Socr
| Line 4: | Line 4: | ||
=== Estimating Population Variance and Standard Deviation=== | === Estimating Population Variance and Standard Deviation=== | ||
| - | The most unbiased point estimate for the population variance <math>\sigma | + | The most unbiased point estimate for the population variance <math>\sigma^2</math> is the [[AP_Statistics_Curriculum_2007_EDA_Var | sample-variance (s<sup>2</sup>)]] and the point estimate for the population standard deviation <math>\sigma</math> is the [[AP_Statistics_Curriculum_2007_EDA_Var | sample standard deviation (s)]]. |
| - | We use a [http://en.wikipedia.org/wiki/Chi_square_distribution Chi-square distribution] to construct confidence intervals for the variance and standard distribution. If the random variable | + | We use a [http://en.wikipedia.org/wiki/Chi_square_distribution Chi-square distribution] to construct confidence intervals for the variance and standard distribution. If the process or phenomenon we study generates a Normal random variable, then computing the following random variable (for a sample of size <math>n>1</math>) has a Chi-square distribution |
| - | + | : <math>\chi_o^2 = {(n-1)s^2 \over \sigma^2}</math> | |
| - | Properties | + | |
| - | + | ===Chi-square Distribution Properties=== | |
| - | + | * All chi-squares values <math>\chi_o^2 \geq 0</math>. | |
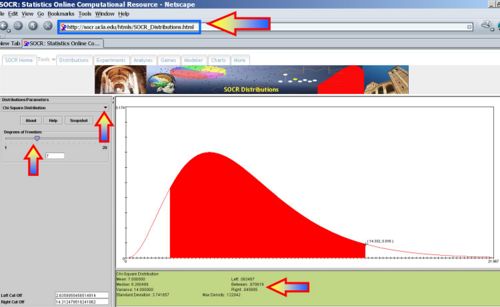
| - | + | * The chi-square distribution is a family of curves, each determined by the degrees of freedom (n-1). See the interactive [http://socr.ucla.edu/htmls/SOCR_Distributions.html Chi-Square distribution]. | |
| - | + | * To form a confidence interval for the variance (<math>\sigma^2</math>), use the <math>\chi^2(df=n-1)</math> distribution with degrees of freedom equal to one less than the sample size. | |
| - | + | * The area under each curve of the Chi-square distribution equals one. | |
| + | * All Chi-square distributions are positively skewed. | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Estim_Var_020408_Fig1.jpg|500px]]</center> | ||
Revision as of 17:50, 4 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Estimating Population Variance
In manufacturing, and many other fields, controlling the amount of variance in producing machinery parts is very important. It is important that the parts vary little or not at all.
Estimating Population Variance and Standard Deviation
The most unbiased point estimate for the population variance σ2 is the sample-variance (s2) and the point estimate for the population standard deviation σ is the sample standard deviation (s).
We use a Chi-square distribution to construct confidence intervals for the variance and standard distribution. If the process or phenomenon we study generates a Normal random variable, then computing the following random variable (for a sample of size n > 1) has a Chi-square distribution
Chi-square Distribution Properties
- All chi-squares values
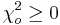 .
.
- The chi-square distribution is a family of curves, each determined by the degrees of freedom (n-1). See the interactive Chi-Square distribution.
- To form a confidence interval for the variance (σ2), use the χ2(df = n − 1) distribution with degrees of freedom equal to one less than the sample size.
- The area under each curve of the Chi-square distribution equals one.
- All Chi-square distributions are positively skewed.
Approach
Models & strategies for solving the problem, data understanding & inference.
- TBD
Model Validation
Checking/affirming underlying assumptions.
- TBD
Computational Resources: Internet-based SOCR Tools
- TBD
Examples
Computer simulations and real observed data.
- TBD
Hands-on activities
Step-by-step practice problems.
- TBD
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: