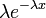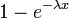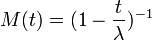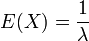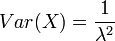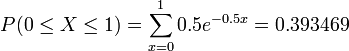AP Statistics Curriculum 2007 Exponential
From Socr
| Line 59: | Line 59: | ||
* SOCR Home page: http://www.socr.ucla.edu | * SOCR Home page: http://www.socr.ucla.edu | ||
| - | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php/ | + | {{translate|pageName=http://wiki.stat.ucla.edu/socr/index.php/AP_Statistics_Curriculum_2007_Exponential}} |
Current revision as of 22:33, 18 July 2011
Contents |
General Advance-Placement (AP) Statistics Curriculum - Exponential Distribution
Exponential Distribution
Definition: Exponential distribution is a special case of the gamma distribution. Whereas the gamma distribution is the waiting time for more than one event, the exponential distribution describes the time between a single Poisson event.
Probability density function: For  , the exponential probability density function is given by
, the exponential probability density function is given by
where
- e is the natural number (e = 2.71828…)
- λ is the mean time between events
- x is a random variable
Cumulative density function: The exponential cumulative distribution function is given by
where
- e is the natural number (e = 2.71828…)
- λ is the mean time between events
- x is a random variable
Moment generating function: The exponential moment-generating function is
Expectation: The expected value of a exponential distributed random variable x is
Variance: The exponential variance is
Applications
The exponential distribution occurs naturally when describing the waiting time in a homogeneous Poisson process. It can be used in a range of disciplines including queuing theory, physics, reliability theory, and hydrology. Examples of events that may be modeled by exponential distribution include:
- The time until a radioactive particle decays
- The time between clicks of a Geiger counter
- The time until default on payment to company debt holders
- The distance between roadkills on a given road
- The distance between mutations on a DNA strand
- The time it takes for a bank teller to serve a customer
- The height of various molecules in a gas at a fixed temperature and pressure in a uniform gravitational field
- The monthly and annual maximum values of daily rainfall and river discharge volumes
Example
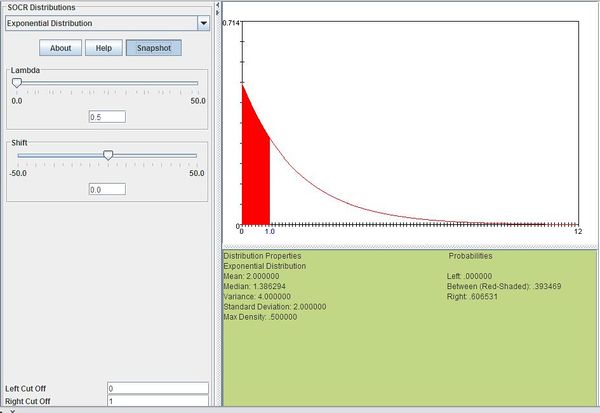
Suppose you usually get 2 phone calls per hour. Compute the probability that a phone call will arrive within the next hour.
2 phone calls per hour means that we would expect one phone call every 1/2 hour so λ = 0.5. We can then compute this as follows:
The figure below shows this result using SOCR distributions
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: