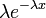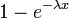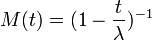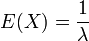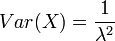AP Statistics Curriculum 2007 Exponential
From Socr
Exponential Distribution
Definition: Exponential distribution is a special case of the gamma distribution. Whereas the gamma distribution is the waiting time for more than one event, the exponential distribution describes the time between a single Poisson event.
Probability density function: For X~Exponential(λ), the exponential probability density function is given by
where
- e is the natural number (e = 2.71828…)
- λ is the mean time between events
- x is a random variable
Cumulative density function: The exponential cumulative distribution function is given by
where
- e is the natural number (e = 2.71828…)
- λ is the mean time between events
- x is a random variable
Moment generating function: The exponential moment-generating function is
Expectation: The expected value of a exponential distributed random variable x is
Variance: The exponential variance is