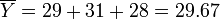AP Statistics Curriculum 2007 Fisher F
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Fisher's F Distribution
Fisher's F Distribution
Commonly used as the null distribution of a test statistic, such as in analysis of variance (ANOVA). Relationship to the t-distribution and [beta Distribution].
PDF:
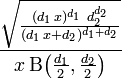
CDF:
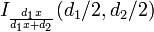
Mean:
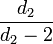 for d2 > 2
for d2 > 2
Median:
None
Variance:
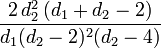 for d2 > 4
for d2 > 4
Support:
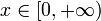
Applications
Example
We want to examine the effect of three different brands of gasoline on gas mileage using an alpha value of 0.05. We will have 6 observations for each of the 3 gasoline brands. Gas mileage figures are as follows:
| Brand A | Brand B | Brand C |
|---|---|---|
| 29 | 30 | 28 |
| 30 | 31 | 29 |
| 29 | 32 | 28 |
| 28 | 29 | 26 |
| 30 | 31 | 30 |
| 28 | 33 | 29 |
Our null hypothesis, H0, is that the three brands of gasoline will yield the same amount of gas mileage, on average.
First, we find the F-ratio:
Step 1: Calculate the mean for each brand:
Brand A: 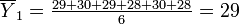
Brand B: 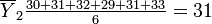
Brand C: 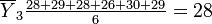
Step 2: Calculate the overall mean:
Step 3: Calculate the Between-Group Sum of Squares:
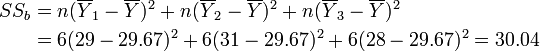
Where n is the number of observations per group.
The between-group degrees of freedom is one less than the number of groups: 3-1=2.
Therefore, the between-group mean square value, MSB, is 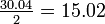
Step 4: Calculate the Within-Group Sum of Squares:
We start by subtracting each observation by its group mean:
| Brand A | Brand B | Brand C |
|---|---|---|
| 29-29=0 | 30-31=-1 | 28-28=0 |
| 30-29=1 | 31-31=0 | 29-28=1 |
| 29-29=0 | 32-31=1 | 28-28=0 |
| 28-29=-1 | 29-31=-2 | 26-28=-2 |
| 30-29=1 | 31-31=0 | 30-28=2 |
| 28-29=-1 | 33-31=2 | 29-28=1 |
The Within-Group Sum of Squares, SSw, is the sum of the squares of the values in the previous table:
0 + 1 + 0 + 1 + 0 + 1 + 0 + 1 + 0 + 1 + 4 + 4 + 1 + 0 + 4 + 1 + 4 + 1 = 24
The Within-Group degrees of freedom is the number of groups times 1 less the number of observations per group:
3(6 − 1) = 15
The Within-Group Mean Square Value, MSW is: 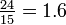
Step 5: Finally, the F-Ratio is:
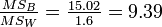
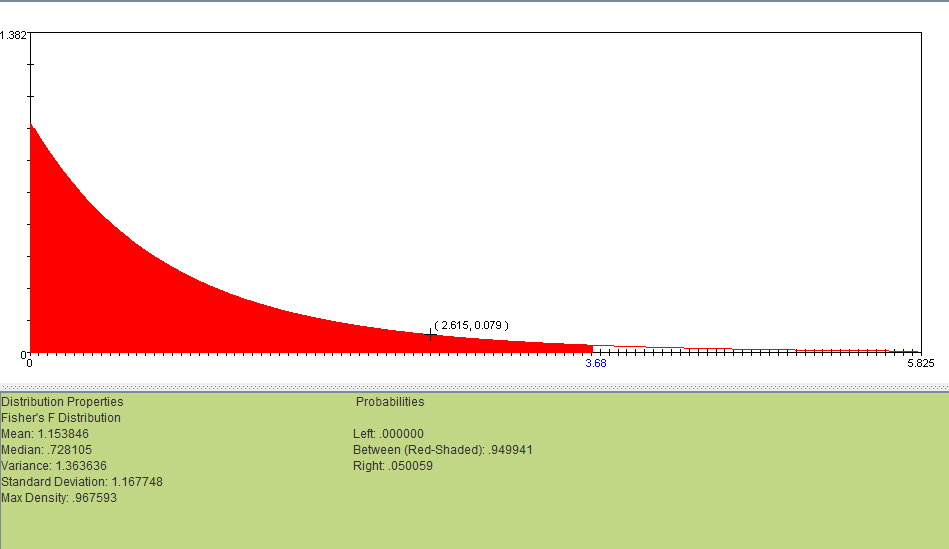
The F critical value is the value that the test statistic must exceed in order to reject the H0. In this case, Fcrit(2,15) = 3.68 at α = 0.05. Since F=9.39>3.68, we reject H0 at the 5% significance level, concluding that there is a difference in gas mileage between the gasoline brands.
We can find the critical F-value using the SOCR F Distribution Calculator:
SOCR Links
http://www.distributome.org/ -> SOCR -> Distributions -> Fisher’s F
http://www.distributome.org/ -> SOCR -> Distributions -> Fisher’s F Distribution
http://www.distributome.org/ -> SOCR -> Functors -> Fisher’s F Distribution
http://www.distributome.org/ -> SOCR -> Analyses -> ANOVA – One Way
http://www.distributome.org/ -> SOCR -> Analyses -> ANOVA – Two Way
SOCR F-Distribution Calculator (http://socr.ucla.edu/htmls/dist/Fisher_Distribution.html)