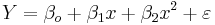AP Statistics Curriculum 2007 GLM MultLin
From Socr
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Multiple Linear Regression == | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Multiple Linear Regression == | ||
| + | |||
| + | In the previous sections we saw how to study the relations in bivariate designs. Now we extend that to any finite number of varaibles (mulitvariate case). | ||
=== Multiple Linear Regression === | === Multiple Linear Regression === | ||
| - | + | We are interested in determining the '''linear regression''', as a model, of the relationship between one '''dependent''' variable ''Y'' and many '''independent''' variables ''X''<sub>''i''</sub>, ''i'' = 1, ..., ''p''. The multilinear regression model can be written as | |
| - | < | + | |
| + | : <math>Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots +\beta_p X_p + \varepsilon</math>, where <math>\varepsilon</math> is the error term. | ||
| + | |||
| + | The coefficient <math>\beta_0</math> is the intercept ("constant" term) and <math>\beta_i</math>s are the respective parameters of the '' p'' independent variables. There are ''p+1'' parameters to be estimated in the multilinear regression. | ||
| + | |||
| + | * Multilinear vs. non-linear regression: This multilinear regression method is "linear" because the relation of the response (the dependent variable <math>Y</math>) to the independent variables is assumed to be a [http://en.wikipedia.org/wiki/Linear_function linear function] of the parameters <math>\beta_i</math>. Note that multilinear regression is a linear modeling technique '''not''' because is that the graph of <math>Y = \beta_{0}+\beta x </math> is a straight line '''nor''' because <math>Y</math> is a linear function of the ''X'' variables. But the "linear" terms refers to the fact that <math>Y</math> can be considered a linear function of the parameters ( <math>\beta_i</math>), even though it is not a linear function of <math>X</math>. Thus, any model like | ||
| + | |||
| + | : <math>Y = \beta_o + \beta_1 x + \beta_2 x^2 + \varepsilon</math> | ||
| + | |||
| + | is still one of '''linear''' regression, that is, linear in <math>x</math> and <math>x^2</math> respectively, even though the graph on <math>x</math> by itself is not a straight line. | ||
===Approach=== | ===Approach=== | ||
Revision as of 00:24, 19 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Multiple Linear Regression
In the previous sections we saw how to study the relations in bivariate designs. Now we extend that to any finite number of varaibles (mulitvariate case).
Multiple Linear Regression
We are interested in determining the linear regression, as a model, of the relationship between one dependent variable Y and many independent variables Xi, i = 1, ..., p. The multilinear regression model can be written as
-
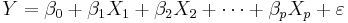 , where
, where 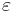 is the error term.
is the error term.
The coefficient β0 is the intercept ("constant" term) and βis are the respective parameters of the p independent variables. There are p+1 parameters to be estimated in the multilinear regression.
- Multilinear vs. non-linear regression: This multilinear regression method is "linear" because the relation of the response (the dependent variable Y) to the independent variables is assumed to be a linear function of the parameters βi. Note that multilinear regression is a linear modeling technique not because is that the graph of Y = β0 + βx is a straight line nor because Y is a linear function of the X variables. But the "linear" terms refers to the fact that Y can be considered a linear function of the parameters ( βi), even though it is not a linear function of X. Thus, any model like
is still one of linear regression, that is, linear in x and x2 respectively, even though the graph on x by itself is not a straight line.
Approach
Models & strategies for solving the problem, data understanding & inference.
- TBD
Model Validation
Checking/affirming underlying assumptions.
- TBD
Computational Resources: Internet-based SOCR Tools
- TBD
Examples
Computer simulations and real observed data.
- TBD
Hands-on activities
Step-by-step practice problems.
- TBD
References
- TBD
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: