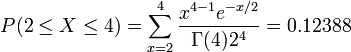AP Statistics Curriculum 2007 Gamma
From Socr
(→Example) |
(→Gamma Distribution) |
||
| Line 4: | Line 4: | ||
<br />'''Probability density function''': The waiting time until the hth Poisson event with a rate of change <math>\lambda</math> is | <br />'''Probability density function''': The waiting time until the hth Poisson event with a rate of change <math>\lambda</math> is | ||
| - | + | <center><math>P(x)=\frac{\lambda(\lambda x)^{h-1}}{(h-1)!}{e^{-\lambda x}}</math></center> | |
For X~Gamma(k,<math>\theta</math>), where <math>k=h</math> and <math>\theta=1/\lambda</math>, the gamma probability density function is given by | For X~Gamma(k,<math>\theta</math>), where <math>k=h</math> and <math>\theta=1/\lambda</math>, the gamma probability density function is given by | ||
| - | + | <center><math>\frac{x^{k-1}e^{-x/\theta}}{\Gamma(k)\theta^k}</math></center> | |
where | where | ||
| Line 19: | Line 19: | ||
<br />'''Cumulative density function''': The gamma cumulative distribution function is given by | <br />'''Cumulative density function''': The gamma cumulative distribution function is given by | ||
| - | + | <center><math>\frac{\gamma(k,x/\theta)}{\Gamma(k)}</math></center> | |
where | where | ||
| Line 26: | Line 26: | ||
<br />'''Moment generating function''': The gamma moment-generating function is | <br />'''Moment generating function''': The gamma moment-generating function is | ||
| - | + | <center><math>M(t)=(1-\theta t)^{-k}\!</math></center> | |
<br />'''Expectation''': The expected value of a gamma distributed random variable x is | <br />'''Expectation''': The expected value of a gamma distributed random variable x is | ||
| - | + | <center><math>E(X)=k\theta\!</math></center> | |
<br />'''Variance''': The gamma variance is | <br />'''Variance''': The gamma variance is | ||
| - | + | <center><math>Var(X)=k\theta^2\!</math></center> | |
| - | + | ||
===Applications=== | ===Applications=== | ||
Revision as of 18:31, 11 July 2011
Gamma Distribution
Definition: Gamma distribution is a distribution that arises naturally in processes for which the waiting times between events are relevant. It can be thought of as a waiting time between Poisson distributed events.
Probability density function: The waiting time until the hth Poisson event with a rate of change λ is
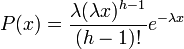
For X~Gamma(k,θ), where k = h and θ = 1 / λ, the gamma probability density function is given by
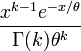
where
- e is the natural number (e = 2.71828…)
- k is the number of occurrences of an event
- if k is a positive integer, then Γ(k) = (k − 1)! is the gamma function
- θ = 1 / λ is the mean number of events per time unit, where λ is the mean time between events. For example, if the mean time between phone calls is 2 hours, then you would use a gamma distribution with θ=1/2=0.5. If we want to find the mean number of calls in 5 hours, it would be 5
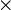 1/2=2.5.
1/2=2.5.
- x is a random variable
Cumulative density function: The gamma cumulative distribution function is given by
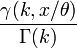
where
- if k is a positive integer, then Γ(k) = (k − 1)! is the gamma function
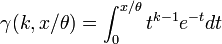
Moment generating function: The gamma moment-generating function is
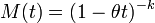
Expectation: The expected value of a gamma distributed random variable x is
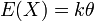
Variance: The gamma variance is
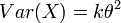
Applications
The gamma distribution can be used a range of disciplines including queuing models, climatology, and financial services. Examples of events that may be modeled by gamma distribution include:
- The amount of rainfall accumulated in a reservoir
- The size of loan defaults or aggregate insurance claims
- The flow of items through manufacturing and distribution processes
- The load on web servers
- The many and varied forms of telecom exchange
The gamma distribution is also used to model errors in a multi-level Poisson regression model because the combination of a Poisson distribution and a gamma distribution is a negative binomial distribution.
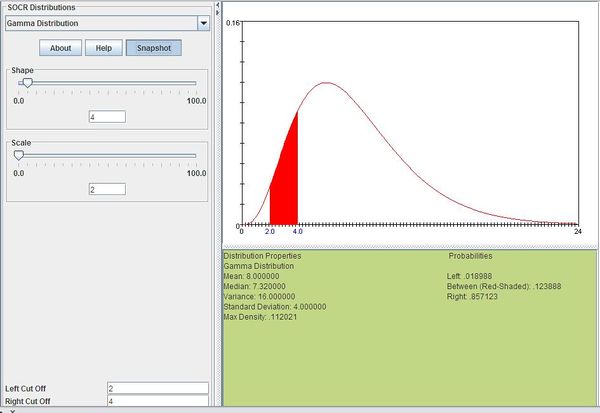
Example
Suppose you are fishing and you expect to get a fish once every 1/2 hour. Compute the probability that you will have to wait between 2 to 4 hours before you catch 4 fish.
One fish every 1/2 hour means we would expect to get θ = 1 / 0.5 = 2 fish every hour on average. Using θ = 2 and k = 4, we can compute this as follows:
The figure below shows this result using SOCR distributions