AP Statistics Curriculum 2007 Hypothesis Basics
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Fundamentals of Hypothesis Testing
Fundamentals of Hypothesis Testing
A (statistical) Hypothesis Test is a method of making statistical decisions about populations or processes based on experimental data. Hypothesis testing just answers the question of how well the findings fit the possibility that chance alone might be responsible for the observed discrepancy between the theoretical model and the empirical observations. This is accomplished by asking and answering a hypothetical question - what is the likelihood of the observed summary statistics of interest, if the data did come from the distribution specified by the null-hypothesis. One use of hypothesis-testing is deciding whether experimental results contain enough information to cast doubt on conventional wisdom.
- Example: Consider determining whether a suitcase contains some radioactive material. Placed under a Geiger counter, the suitcase produces 10 clicks (counts) per minute. The null hypothesis is that there is no radioactive material in the suitcase and that all measured counts are due to ambient radioactivity typical of the surrounding air and harmless objects in a suitcase. We can then calculate how likely it is that the null hypothesis produces 10 counts per minute. If it is likely, for example if the null hypothesis predicts on average 9 counts per minute, we say that the suitcase is compatible with the null hypothesis (which does not imply that there is no radioactive material, we just can't determine from the 1-minute sample we took using this specific method!); On the other hand, if the null hypothesis predicts for example 1 count per minute, then the suitcase is not compatible with the null hypothesis and there must be other factors responsible to produce the increased radioactive counts.
The Hypothesis Testing is also known as Statistical Significance Testing. The null hypothesis is a conjecture that exists solely to be disproved, rejected or falsified by the sample-statistics used to estimate the unknown population parameters. Statistical significance is a possible finding of the test, that the sample is unlikely to have occurred in this process by chance given the truth of the null hypothesis. The name of the test describes its formulation and its possible outcome. One characteristic of hypothesis testing is its crisp decision about the null-hypothesis: reject or do not reject (which is not the same as accept).
Null and Alternative (Research) Hypotheses
A Null Hypothesis is a theses set up to be nullified or refuted in order to support an Alternate (research) Hypothesis. The null hypothesis is presumed true until statistical evidence, in the form of a hypothesis test, indicates otherwise. In science, the null hypothesis is used to test differences between treatment and control groups, and the assumption at the outset of the experiment is that no difference exists between the two groups for the variable of interest (e.g., population means). The null hypothesis proposes something initially presumed true, and it is rejected only when it becomes evidently false. That is, when a researcher has a certain degree of confidence, usually 95% to 99%, that the data do not support the null hypothesis.
Example
If we want to compare the test scores of two random samples of men and women, a null hypothesis would be that the mean score of the male population was the same as the mean score of the female population:
- H0 : μmen = μwomen
where:
- H0 = the null hypothesis
- μmen = the mean of the males (population 1), and
- μwomen = the mean of the females (population 2).
Alternatively, the null hypothesis can postulate that the two samples are drawn from the same population, so that the center, variance and shape of the distributions are equal.
Formulation of the null hypothesis is a vital step in testing statistical significance. Having formulated such a hypothesis, one can establish the probability of observing the obtained data from the prediction of the null hypothesis, if the null hypothesis is true. That probability is what is commonly called the significance level of the results.
In many scientific experimental designs we predict that a particular factor will produce an effect on our dependent variable — this is our alternative hypothesis. We then consider how often we would expect to observe our experimental results, or results even more extreme, if we were to take many samples from a population where there was no effect (i.e. we test against our null hypothesis). If we find that this happens rarely (up to, say, 5% of the time), we can conclude that our results support our experimental prediction — we reject our null hypothesis.
Type I Error, Type II Error and Power
Directly related to hypothesis testing are the following 3 concepts:
- Type I Error: The false positive (Type I) Error of rejecting the null hypothesis given that it is actually true; e.g., A court finding a person guilty of a crime that they did not actually commit.
- Type II Error: The Type II Error (false negative) is the error of failing to reject the null hypothesis given that the alternative hypothesis is actually true; e.g., A court finding a person not guilty of a crime that they did actually commit.
- Statistical Power: The Power of a Statistical Test is the probability that the test will reject a false null hypothesis (that it will not make a Type II Error). As power increases, the chances of a Type II error decrease. The probability of a Type II error is referred to as the false negative rate (β). Therefore power is equal to 1 − β. You can also see this SOCR Power Activity.
| Actual condition | |||
|---|---|---|---|
| Absent (Ho is true) | Present (H1 is true) | ||
| Test Result | Negative (fail to reject Ho) | Condition absent + Negative result = True (accurate) Negative (TN, 0.98505) | Condition present + Negative result = False (invalid) Negative (FN, 0.00025) Type II error (β) |
| Positive (reject Ho) | Condition absent + Positive result = False Positive (FP, 0.00995) Type I error (α) | Condition Present + Positive result = True Positive (TP, 0.00475) | |
| Test Interpretation | Power = 1-FN= 1-0.00025 = 0.99975 | Specificity: TN/(TN+FP) = 0.98505/(0.98505+ 0.00995) = 0.99 | Sensitivity: TP/(TP+FN) = 0.00475/(0.00475+ 0.00025)= 0.95 |
- Remarks:
- A Specificity of 100% means that the test recognizes all healthy individuals as (normal) healthy. The maximum is trivially achieved by a test that claims everybody is healthy regardless of the true condition. Therefore, the specificity alone does not tell us how well the test recognizes positive cases.
- False positive rate (α)= FP/(FP+TN) = 0.00995/(0.00995 + 0.98505)=0.01 = 1 - Specificity.
- Sensitivity is a measure of how well a test correctly identifies a condition, whether this is medical screening tests picking up on a disease, or quality control in factories deciding if a new product is good enough to be sold.
- False Negative Rate (β)= FN/(FN+TP) = 0.00025/(0.00025+0.00475)=0.05 = 1 - Sensitivity.
- Power = 1 − β= 0.95, see Power_Analysis_for_Normal_Distribution.
Example
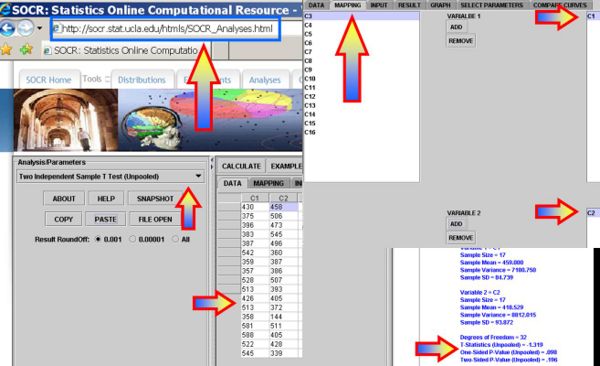
Use the Hot-dog dataset to see if there is statistically significant difference in the sodium content of the poultry vs. meat hotdogs.
- Formulate Hypotheses: Ho:μp = μm vs.
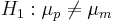 , where μp,μm represent the mean sodium content in poultry and mean hotdogs, respectively.
, where μp,μm represent the mean sodium content in poultry and mean hotdogs, respectively.
- Plug in the data in SOCR Analyses under the Two Independent Sample T-Test (Unpooled) will generate results as shown on the figure below (Two-Sided P-Value (Unpooled) = 0.196, which does not provide strong evidence to reject the null hypothesis that the two types of hot-dogs have the same mean sodium content)
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
