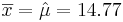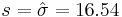AP Statistics Curriculum 2007 Hypothesis L Mean
From Socr
m (→Hypothesis Testing About a Mean: Large Samples) |
|||
| (26 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Testing a Claim | + | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Testing a Claim About a Mean: Large Samples== |
| - | We already saw [[AP_Statistics_Curriculum_2007_Estim_L_Mean | how to construct point and interval estimates for the population mean in the large sample case]]. Now, we show how to do hypothesis | + | We already saw [[AP_Statistics_Curriculum_2007_Estim_L_Mean | how to construct point and interval estimates for the population mean in the large sample case]]. Now, we show how to do hypothesis testing of the mean for large sample-sizes. |
===[[AP_Statistics_Curriculum_2007_Estim_L_Mean | Background]]=== | ===[[AP_Statistics_Curriculum_2007_Estim_L_Mean | Background]]=== | ||
| - | * Recall that the population mean may be estimated by the sample average, <math>\overline{X_n}={1\over n}\sum_{i=1}^n{X_i}</math> | + | * Recall that for a random sample {<math>X_1, X_2, X_3, \cdots , X_n</math>} of the process, the population mean may be estimated by the sample average, <math>\overline{X_n}={1\over n}\sum_{i=1}^n{X_i}</math>. |
* For a given small <math>\alpha</math> (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.), the <math>(1-\alpha)100%</math> Confidence interval for the mean is constructed by | * For a given small <math>\alpha</math> (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.), the <math>(1-\alpha)100%</math> Confidence interval for the mean is constructed by | ||
| Line 13: | Line 13: | ||
: and <math>z_{\alpha\over 2}</math> is the [[AP_Statistics_Curriculum_2007_Normal_Critical | critical value]] for a [[AP_Statistics_Curriculum_2007_Normal_Std |Standard Normal]] distribution at <math>{\alpha\over 2}</math>. | : and <math>z_{\alpha\over 2}</math> is the [[AP_Statistics_Curriculum_2007_Normal_Critical | critical value]] for a [[AP_Statistics_Curriculum_2007_Normal_Std |Standard Normal]] distribution at <math>{\alpha\over 2}</math>. | ||
| - | === Hypothesis Testing | + | === Hypothesis Testing About a Mean: Large Samples=== |
| - | * Null Hypothesis: <math>H_o: \mu=\mu_o</math> (e.g., 0) | + | * Null Hypothesis: <math>H_o: \mu=\mu_o</math> (e.g., <math>\mu_o=0</math>) |
* Alternative Research Hypotheses: | * Alternative Research Hypotheses: | ||
| - | ** One sided (uni-directional): <math>H_1: \mu >\mu_o</math>, or <math> | + | ** One sided (uni-directional): <math>H_1: \mu >\mu_o</math>, or <math>H_1: \mu<\mu_o</math> |
| - | ** Double sided: | + | ** Double sided: \(H_1: \mu \not= \mu_o\) |
====Known Variance==== | ====Known Variance==== | ||
| - | * [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test | + | * [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test Statistics]: |
| - | : <math>Z_o = {\overline{x} - \mu_o \over \sigma} \sim N(0,1)</math>. | + | : <math>Z_o = {\overline{x} - \mu_o \over {\sigma \over \sqrt{n}}} \sim N(0,1)</math>. |
====Unknown Variance==== | ====Unknown Variance==== | ||
| - | * [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test | + | * [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test Statistics]: |
| - | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {\overline{x} - \mu_o \over {{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}})} \sim | + | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {\overline{x} - \mu_o \over {{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}})} \sim T_{(df=n-1)}</math>. |
===Example=== | ===Example=== | ||
| - | Let's [[AP_Statistics_Curriculum_2007_Estim_L_Mean | revisit the ''number of sentences per advertisement'' example]], where we measure | + | Let's [[AP_Statistics_Curriculum_2007_Estim_L_Mean#Example | revisit the ''number of sentences per advertisement'' example]], where we measure the readability for magazine advertisements. A random sample of the number of sentences found in 30 magazine advertisements is listed below. Suppose: |
| + | : We want to test at <math>\alpha=0.05</math> | ||
| + | : Null hypothesis: <math>H_o: \mu=20</math> | ||
| + | : Against a double-sided research alternative hypothesis: <math>H_1: \mu \not= 20</math>. | ||
| + | |||
<center> | <center> | ||
{| class="wikitable" style="text-align:center; width:75%" border="1" | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| Line 40: | Line 44: | ||
: <math>s=\hat{\sigma}=16.54</math> | : <math>s=\hat{\sigma}=16.54</math> | ||
| - | As the population variance is not given, we have to use the [[AP_Statistics_Curriculum_2007_StudentsT |T- | + | As the population variance is not given, we have to use the [[AP_Statistics_Curriculum_2007_StudentsT |T-Statistics]]: <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} \sim T(df=29)</math> |
| - | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {14.77 - 20 \over {{1\over \sqrt{30}} \sqrt{\sum_{i=1}^{30}{(x_i-14.77)^2\over 29}}})} | + | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {14.77 - 20 \over {{1\over \sqrt{30}} \sqrt{\sum_{i=1}^{30}{(x_i-14.77)^2\over 29}}})}=-1.733</math>. |
| + | : <math>P(T_{(df=29)} < T_o=-1.733)=0.047</math>, thus | ||
| + | : the <math>p-value=2\times 0.047= 0.094</math> for this (double-sided) test. | ||
| - | == | + | Therefore, we '''can not reject''' the null hypothesis at <math>\alpha=0.05</math>! The left and right white areas at the tails of the T(df=29) distribution depict graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, the cumulative tail area is 0.094, which is larger than the initially set [[AP_Statistics_Curriculum_2007_Hypothesis_Basics | Type I]] error <math>\alpha = 0.05</math> so we can not reject the null hypothesis. |
| - | + | <center>[[Image:SOCR_EBook_Dinov_Hypothesis_020508_Fig3.jpg|600px]]</center> | |
| - | * | + | |
| - | <center>[[Image: | + | * You can use the [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses (One-Sample T-Test)] to carry out these calculations as shown in the figure below. |
| - | [[ | + | <center>[[Image:SOCR_EBook_Dinov_Hypothesis_020508_Fig2.jpg|600px]]</center> |
| + | |||
| + | * This [[SOCR_EduMaterials_AnalysisActivities_OneT | SOCR One Sample T-test Activity]] provides additional hands-on demonstrations of one-sample hypothesis testing. | ||
| + | |||
| + | ===Examples=== | ||
| + | |||
| + | ====Cavendish Mean Density of the Earth==== | ||
| + | A number of famous early experiments of measuring physical constants has later been shown to be biased. In the 1700's [http://en.wikipedia.org/wiki/Henry_Cavendish Henry Cavendish] measured the [http://www.jstor.org/stable/pdfplus/107617.pdf Mean density of the Earth]. Formulate and test null and research hypotheses about these data regarding the now known exact mean-density value = 5.517. These sample statistics may be helpful (you can also find the [[AP_Statistics_Curriculum_2007_Hypothesis_L_Mean_Tbl1_tr|transposed table here]]): | ||
| + | : n = 23, sample mean = 5.483, sample SD = 0.1904 | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:75%" border="1" | ||
| + | |- | ||
| + | | 5.36 || 5.29 || 5.58 || 5.65 || 5.57 || 5.53 || 5.62 || 5.29 || 5.44 || 5.34 || 5.79 || 5.10 || 5.27 || 5.39 || 5.42 || 5.47 || 5.63 || 5.34 || 5.46 || 5.30 || 5.75 || 5.68 || 5.85 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | ====US Federal Budget Deficit==== | ||
| + | Use the [[SOCR_Data_US_BudgetsDeficits_1849_2016 | US Federal Budget Deficit data (1849-2016)]] to formulate and test several Null hypotheses on whether the US Federal Budget Deficit is trivial (<math>\mu_o=0</math>) in different time frames (e.g., 1849-2000 or 1900-2016). Start with some [[AP_Statistics_Curriculum_2007_EDA_Plots |exploratory data analyses]] to plot the data as shown in the [[SOCR_Data_US_BudgetsDeficits_1849_2016|data page]]. Then you can use the [http://www.socr.ucla.edu/htmls/ana/OneSampleTTest_Analysis.html SOCR One Sample T-Test] and the [http://www.socr.ucla.edu/htmls/ana/ConfidenceInterval_Analysis.html SOCR Confidence Interval] applets. What are your conclusions? | ||
<hr> | <hr> | ||
| - | === | + | ===Hypothesis Testing Summary=== |
| + | Important parts of Hypothesis Test conclusions: | ||
| + | * Decision (significance or no significance) | ||
| + | * Parameter of Interest | ||
| + | * Variable of Interest | ||
| + | * Population under study | ||
| + | * (optional but preferred) P-value | ||
| + | |||
| + | === Parallels between Hypothesis Testing and Confidence Intervals=== | ||
| + | These are different methods for coping with the uncertainty about the true value of a parameter caused by the sampling variation in estimates. | ||
| + | |||
| + | * [[AP_Statistics_Curriculum_2007_Estim_L_Mean | Confidence Intervals]]: A fixed level of confidence is chosen. We determine a range of possible values for the parameter that are consistent with the data (at the chosen confidence level). | ||
| + | |||
| + | * Hypothesis (Significance) testing: Only one possible value for the parameter, called the hypothesized value, is tested. We determine the strength of the evidence (confidence) provided by the data against the proposition that the hypothesized value is the true value. | ||
| + | |||
| + | ===[[EBook_Problems_Hypothesis_L_Mean|Problems]]=== | ||
<hr> | <hr> | ||
Current revision as of 15:48, 22 May 2013
Contents
|
General Advance-Placement (AP) Statistics Curriculum - Testing a Claim About a Mean: Large Samples
We already saw how to construct point and interval estimates for the population mean in the large sample case. Now, we show how to do hypothesis testing of the mean for large sample-sizes.
Background
- Recall that for a random sample {
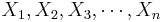 } of the process, the population mean may be estimated by the sample average,
} of the process, the population mean may be estimated by the sample average, 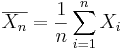 .
.
- For a given small α (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.), the (1 − α)100% Confidence interval for the mean is constructed by
-
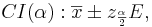
- where the margin of error E is defined as
-
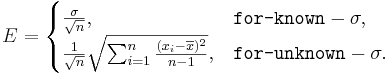
- and
 is the critical value for a Standard Normal distribution at
is the critical value for a Standard Normal distribution at 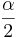 .
.
Hypothesis Testing About a Mean: Large Samples
- Null Hypothesis: Ho:μ = μo (e.g., μo = 0)
- Alternative Research Hypotheses:
- One sided (uni-directional): H1:μ > μo, or H1:μ < μo
- Double sided: \(H_1: \mu \not= \mu_o\)
Known Variance
-
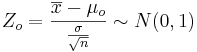 .
.
Unknown Variance
-
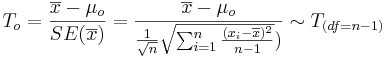 .
.
Example
Let's revisit the number of sentences per advertisement example, where we measure the readability for magazine advertisements. A random sample of the number of sentences found in 30 magazine advertisements is listed below. Suppose:
- We want to test at α = 0.05
- Null hypothesis: Ho:μ = 20
- Against a double-sided research alternative hypothesis:
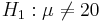 .
.
| 16 | 9 | 14 | 11 | 17 | 12 | 99 | 18 | 13 | 12 | 5 | 9 | 17 | 6 | 11 | 17 | 18 | 20 | 6 | 14 | 7 | 11 | 12 | 5 | 18 | 6 | 4 | 13 | 11 | 12 |
We had the following 2 sample statistics computed earlier
As the population variance is not given, we have to use the T-Statistics: 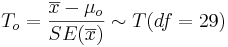
-
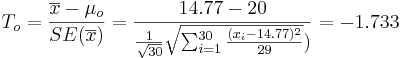 .
.
- P(T(df = 29) < To = − 1.733) = 0.047, thus
- the
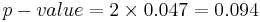 for this (double-sided) test.
for this (double-sided) test.
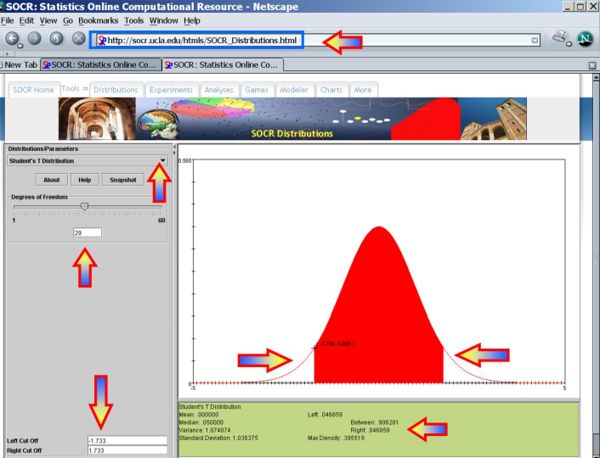
Therefore, we can not reject the null hypothesis at α = 0.05! The left and right white areas at the tails of the T(df=29) distribution depict graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, the cumulative tail area is 0.094, which is larger than the initially set Type I error α = 0.05 so we can not reject the null hypothesis.
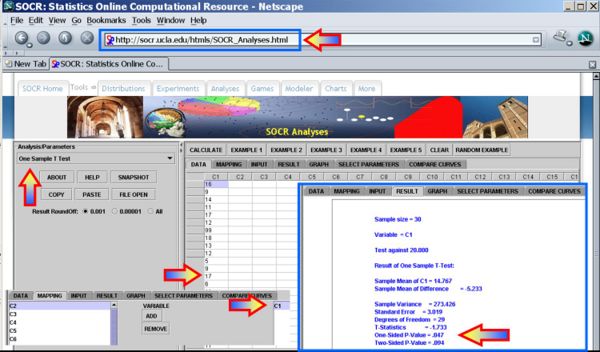
- You can use the SOCR Analyses (One-Sample T-Test) to carry out these calculations as shown in the figure below.
- This SOCR One Sample T-test Activity provides additional hands-on demonstrations of one-sample hypothesis testing.
Examples
Cavendish Mean Density of the Earth
A number of famous early experiments of measuring physical constants has later been shown to be biased. In the 1700's Henry Cavendish measured the Mean density of the Earth. Formulate and test null and research hypotheses about these data regarding the now known exact mean-density value = 5.517. These sample statistics may be helpful (you can also find the transposed table here):
- n = 23, sample mean = 5.483, sample SD = 0.1904
| 5.36 | 5.29 | 5.58 | 5.65 | 5.57 | 5.53 | 5.62 | 5.29 | 5.44 | 5.34 | 5.79 | 5.10 | 5.27 | 5.39 | 5.42 | 5.47 | 5.63 | 5.34 | 5.46 | 5.30 | 5.75 | 5.68 | 5.85 |
US Federal Budget Deficit
Use the US Federal Budget Deficit data (1849-2016) to formulate and test several Null hypotheses on whether the US Federal Budget Deficit is trivial (μo = 0) in different time frames (e.g., 1849-2000 or 1900-2016). Start with some exploratory data analyses to plot the data as shown in the data page. Then you can use the SOCR One Sample T-Test and the SOCR Confidence Interval applets. What are your conclusions?
Hypothesis Testing Summary
Important parts of Hypothesis Test conclusions:
- Decision (significance or no significance)
- Parameter of Interest
- Variable of Interest
- Population under study
- (optional but preferred) P-value
Parallels between Hypothesis Testing and Confidence Intervals
These are different methods for coping with the uncertainty about the true value of a parameter caused by the sampling variation in estimates.
- Confidence Intervals: A fixed level of confidence is chosen. We determine a range of possible values for the parameter that are consistent with the data (at the chosen confidence level).
- Hypothesis (Significance) testing: Only one possible value for the parameter, called the hypothesized value, is tested. We determine the strength of the evidence (confidence) provided by the data against the proposition that the hypothesized value is the true value.
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: