AP Statistics Curriculum 2007 Hypothesis L Mean
From Socr
Contents |
General Advance-Placement (AP) Statistics Curriculum - Testing a Claim about a Mean: Large Samples
We already saw how to construct point and interval estimates for the population mean in the large sample case. Now, we show how to do hypothesis tests about the mean in as the sample-sizes are large.
Background
- Recall that the population mean may be estimated by the sample average,
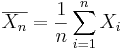 , of random sample {
, of random sample {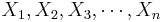 } of the procees.
} of the procees.
- For a given small α (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.), the (1 − α)100% Confidence interval for the mean is constructed by
-
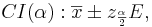
- where the margin of error E is defined as
-
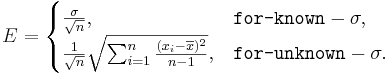
- and
 is the critical value for a Standard Normal distribution at
is the critical value for a Standard Normal distribution at 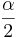 .
.
Hypothesis Testing about a Mean: Large Samples
- Null Hypothesis: Ho:μ = μo (e.g., 0)
- Alternative Research Hypotheses:
- One sided (uni-directional): H1:μ > μo, or Ho:μ < μo
- Double sided:
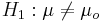
Known Variance
-
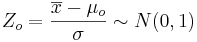 .
.
Unknown Variance
-
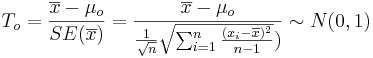 .
.
Example
Let's revisit the number of sentences per advertisement example, where we measure of readability for magazine advertisements. A random sample of the number of sentences found in 30 magazine advertisements is listed below. Suppose we want to test a null hypothesis: Ho:μ = 20 against a double-sided research alternative hypothesis: 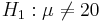 .
.
| 16 | 9 | 14 | 11 | 17 | 12 | 99 | 18 | 13 | 12 | 5 | 9 | 17 | 6 | 11 | 17 | 18 | 20 | 6 | 14 | 7 | 11 | 12 | 5 | 18 | 6 | 4 | 13 | 11 | 12 |
We had the following 2 sample statistics computed earlier
As the population variance is not given, we have to use the T-statistics
-
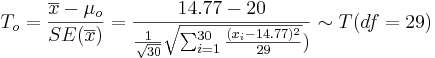 .
.
Hands-on activities
- See the SOCR Confidence Interval Experiment.
- Sample statistics, like the sample-mean and the sample-variance, may be easily obtained using SOCR Charts. The images below illustrate this functionality (based on the Bar-Chart and Index-Chart) using the 30 observations of the number of sentences per advertisement, reported above.
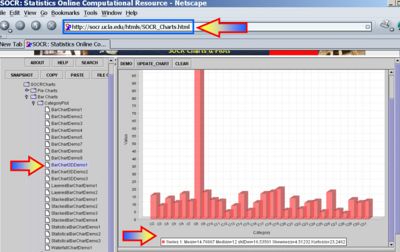
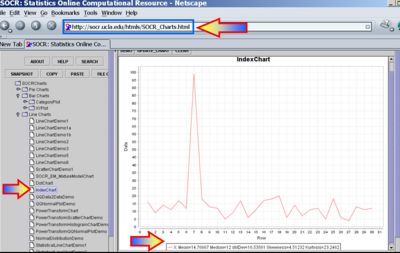
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page: