AP Statistics Curriculum 2007 Hypothesis S Mean
From Socr
m (→Hypothesis Testing about a Mean: Small Samples) |
m (→Example) |
||
| (One intermediate revision not shown) | |||
| Line 24: | Line 24: | ||
====(Approximately) Normal Process with Unknown Variance==== | ====(Approximately) Normal Process with Unknown Variance==== | ||
* If the population is approximately Normally distributed and we do not know the population variance, then the [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test statistics] is: | * If the population is approximately Normally distributed and we do not know the population variance, then the [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test statistics] is: | ||
| - | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {\overline{x} - \mu_o \over {{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}} | + | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {\overline{x} - \mu_o \over {{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}}} \sim T_{(df=n-1)}</math>. |
===Example=== | ===Example=== | ||
| Line 36: | Line 36: | ||
As the population variance is not given, we have to use the [[AP_Statistics_Curriculum_2007_StudentsT |T-statistics]]: <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} \sim T(df=9)</math> | As the population variance is not given, we have to use the [[AP_Statistics_Curriculum_2007_StudentsT |T-statistics]]: <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} \sim T(df=9)</math> | ||
| - | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {22.1 - 12 \over {{1\over \sqrt{10}} \sqrt{\sum_{i=1}^{10}{(x_i-22.1)^2\over 9}}} | + | : <math>T_o = {\overline{x} - \mu_o \over SE(\overline{x})} = {22.1 - 12 \over {{1\over \sqrt{10}} \sqrt{\sum_{i=1}^{10}{(x_i-22.1)^2\over 9}}}}=1.176</math>. |
: <math>p-value=P(T_{(df=9)}>T_o=1.176)=0.134882</math> for this (one-sided) test. Therefore, we '''cannot reject''' the null hypothesis at <math>\alpha=0.01</math>! The left white area at the tails of the T(df=9) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.134882, which is larger than the initially set [[AP_Statistics_Curriculum_2007_Hypothesis_Basics | Type I]] error <math>\alpha = 0.01</math> and we cannot reject the null hypothesis. | : <math>p-value=P(T_{(df=9)}>T_o=1.176)=0.134882</math> for this (one-sided) test. Therefore, we '''cannot reject''' the null hypothesis at <math>\alpha=0.01</math>! The left white area at the tails of the T(df=9) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.134882, which is larger than the initially set [[AP_Statistics_Curriculum_2007_Hypothesis_Basics | Type I]] error <math>\alpha = 0.01</math> and we cannot reject the null hypothesis. | ||
<center>[[Image:SOCR_EBook_Dinov_Hypothesis_020508_Fig4.jpg|600px]]</center> | <center>[[Image:SOCR_EBook_Dinov_Hypothesis_020508_Fig4.jpg|600px]]</center> | ||
Current revision as of 04:36, 7 June 2013
Contents
|
General Advance-Placement (AP) Statistics Curriculum - Testing a Claim about a Mean: Small Samples
Testing a Claim about a Mean: Small Samples
The previous section discussed inference on the population mean for large smaples. Now, we show how to do hypothesis testing of the mean for small sample-sizes.
Background
- Recall that for a random sample {
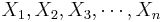 } of the process, the population mean may be estimated by the sample average,
} of the process, the population mean may be estimated by the sample average, 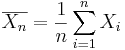 .
.
- For a given small α (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.), the (1 − α)100% Confidence interval for the mean is constructed by
-
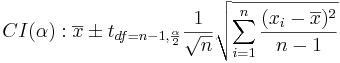
- and
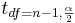 is the critical value for a T-distribution of df=(sample size - 1) at
is the critical value for a T-distribution of df=(sample size - 1) at 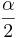 .
.
Hypothesis Testing about a Mean: Small Samples
- Null Hypothesis: Ho:μ = μo (e.g., 0)
- Alternative Research Hypotheses:
- One sided (uni-directional): H1:μ > μo, or Ho:μ < μo
- Double sided: \(H_1: \mu \not= \mu_o\)
Normal Process with Known Variance
- If the population is Normally distributed and we know the population variance, then the Test statistics is:
-
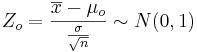 .
.
(Approximately) Normal Process with Unknown Variance
- If the population is approximately Normally distributed and we do not know the population variance, then the Test statistics is:
-
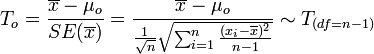 .
.
Example
Let's use again the small-sample example of the number of sentences per advertisement, where we measure the readability for magazine advertisements. A random sample of the number of sentences found in 10 magazine advertisements is listed below. Suppose we want to test at α = 0.01 a null hypothesis: Ho:μ = 12 against a one-sided research alternative hypothesis: H1:μ > 12. Recall that we had the following sample statistics: sample-mean=22.1, sample-variance=737.88 and sample-SD=27.16390579 for these data.
| 16 | 9 | 14 | 11 | 17 | 12 | 99 | 18 | 13 | 12 |
As the population variance is not given, we have to use the T-statistics: 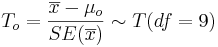
-
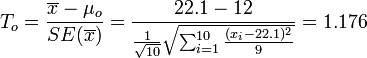 .
.
- p − value = P(T(df = 9) > To = 1.176) = 0.134882 for this (one-sided) test. Therefore, we cannot reject the null hypothesis at α = 0.01! The left white area at the tails of the T(df=9) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.134882, which is larger than the initially set Type I error α = 0.01 and we cannot reject the null hypothesis.
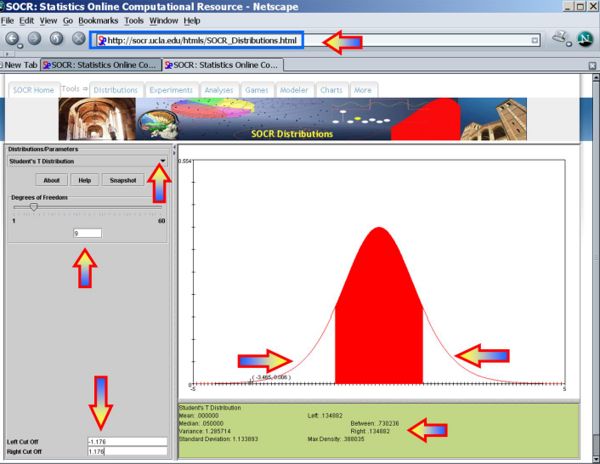
- You can also use the SOCR Analyses (One-Sample T-Test) to carry out these calculations as shown in the figure below.
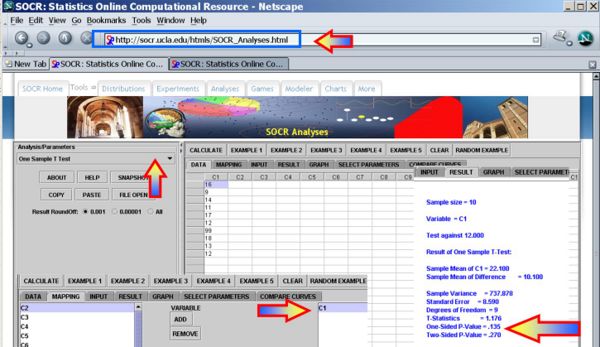
- This SOCR One Smaple T-test Activity provides additional hands-on demonstrations of one-sample hypothesis testing.
Examples
Cavendish Mean Density of the Earth
A number of famous early experiments of measuring physical constants have later been shown to be biased. In the 1700's Henry Cavendish measured the mean density of the Earth. Formulate and test null and research hypotheses about these data regarding the now known exact mean-density value = 5.517. These sample statistics may be helpful
- n = 23, sample mean = 5.483, sample SD = 0.1904
| 5.36 | 5.29 | 5.58 | 5.65 | 5.57 | 5.53 | 5.62 | 5.29 | 5.44 | 5.34 | 5.79 | 5.10 | 5.27 | 5.39 | 5.42 | 5.47 | 5.63 | 5.34 | 5.46 | 5.30 | 5.75 | 5.68 | 5.85 |
Hypothesis Testing Summary
Important parts of Hypothesis test conclusions:
- Decision (significance or no significance)
- Parameter of interest
- Variable of interest
- Population under study
- (optional but preferred) P-value
Parallels between Hypothesis Testing and Confidence Intervals
These are different methods for coping with the uncertainty about the true value of a parameter caused by the sampling variation in estimates.
- Confidence intervals: A fixed level of confidence is chosen. We determine a range of possible values for the parameter that are consistent with the data (at the chosen confidence level).
- Hypothesis (Significance) testing: Only one possible value for the parameter, called the hypothesized value, is tested. We determine the strength of the evidence (confidence) provided by the data against the proposition that the hypothesized value is the true value.
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
