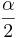AP Statistics Curriculum 2007 Infer 2Means Dep
From Socr
(→Paired vs. Independent Testing) |
|||
| (41 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Inferences about Two Means: Dependent Samples== | ==[[AP_Statistics_Curriculum_2007 | General Advance-Placement (AP) Statistics Curriculum]] - Inferences about Two Means: Dependent Samples== | ||
| - | + | In the [[AP_Statistics_Curriculum_2007_Hypothesis_S_Mean | previous chapter we saw how to do significance testing in the case of a single random sample]]. Now, we show how to do hypothesis testing comparing two samples and we begin with the simple case of paired samples. | |
| - | + | ||
| - | + | ||
| - | === | + | === Inferences About Two Means: Dependent Samples=== |
| - | + | In all study designs, it is always critical to clearly identify whether samples we compare come from dependent or independent populations. There is a general formulation for the significance testing when the samples are independent. The fact that there may be uncountable many different types of dependencies that prevents us from having a similar analysis protocol for ''all'' dependent sample cases. However, in one specific case - paired samples - we have a theory to generalize the significance testing analysis protocol. Two populations (or samples) are ''dependent because of pairing'' (or paired) if they are linked in some way, usually by a direct relationship. For example, measure the weight of subjects before and after a six month diet. | |
| - | + | ===Paired Designs=== | |
| + | These are the most common '''Paired Designs''', in which the idea of pairing is that members of a pair are similar to each other with respect to extraneous variables. | ||
| - | + | *Randomized block experiments with two units per block | |
| - | + | *Observational studies with individually matched controls (e.g., clinical trials of drug efficacy - patient pre vs. post treatment results are compared) | |
| + | *Repeated (time or treatment affected) measurements on the same individual | ||
| + | *Blocking by time – formed implicitly when replicate measurements are made at different times. | ||
| - | * | + | ===[[AP_Statistics_Curriculum_2007_Estim_L_Mean | Background]]=== |
| + | * Recall that for a random sample {<math>X_1, X_2, X_3, \cdots , X_n</math>} of the process, the population mean may be estimated by the sample average, <math>\overline{X_n}={1\over n}\sum_{i=1}^n{X_i}</math>. | ||
| - | = | + | * The standard error of <math>\overline{x}</math> is given by <math>{{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(x_i-\overline{x})^2\over n-1}}}</math>. |
| - | + | ||
| - | === | + | ===Analysis Protocol for Paired Designs=== |
| - | + | To study paired data, we would like to examine the differences between each pair. Suppose {<math>X_1, X_2, X_3, \cdots , X_n</math>} and {<math>Y_1, Y_2, Y_3, \cdots , Y_n</math>} represent the 2 paired samples. Then we want to study the difference sample {<math>d_1=X_1-Y_1, d_2=X_2-Y_2, d_3=X_3-Y_3, \cdots , d_n=X_n-Y_n</math>}. Notice the effect of the pairings of each <math>X_i</math> and <math>Y_i</math>. | |
| - | + | Now we can clearly see that the group effect (group differences) is directly represented in the {<math>d_i</math>} sequence. The [[AP_Statistics_Curriculum_2007_Hypothesis_S_Mean#.28Approximately.29_Nornal_Process_with_Unknown_Variance | one-sample T test]] is the proper strategy to analyze the difference sample {<math>d_i</math>}, if the <math>X_i</math> and <math>Y_i</math> samples come from [[AP_Statistics_Curriculum_2007#Chapter_V:_Normal_Probability_Distribution |Normal distributions]]. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | * | + | Since we are focusing on the differences, we can use the same reasoning as we did in the [[AP_Statistics_Curriculum_2007_Hypothesis_S_Mean#.28Approximately.29_Nornal_Process_with_Unknown_Variance |single sample case]] to calculate the standard error (i.e., the standard deviation of the sampling distribution of <math>\overline{d}</math>) of <math>\overline{d}={1\over n}\sum_{i=1}^n{d_i}</math>. |
| + | |||
| + | Thus, the standard error of <math>\overline{d}</math> is given by <math>{{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(d_i-\overline{d})^2\over n-1}}}</math>, where <math>d_i=X_i-Y_i, \forall 1\leq i\leq n</math>. | ||
| + | |||
| + | ===[[AP_Statistics_Curriculum_2007_Estim_S_Mean | Confidence Interval]] of the Difference of Means=== | ||
| + | The interval estimation of the difference of two means (or '''Confidence intervals''') is constructed as follows. Choose a confidence level <math>(1-\alpha)100%</math>, where <math>\alpha</math> is small (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.). Then a <math>(1-\alpha)100%</math> confidence interval for <math>\mu_1 - \mu_2</math> is defined in terms of the T-distribution: | ||
| + | : <math>CI(\alpha): \overline{x}-\overline{y} \pm t_{\alpha\over 2} SE(\overline {x}-\overline{y}) = \overline{d} \pm t_{\alpha\over 2} {1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(d_i-\overline{d})^2\over n-1}}</math> | ||
| + | |||
| + | * <math>t_{\alpha\over 2}</math> is the [[AP_Statistics_Curriculum_2007_StudentsT | critical value for the T(df=sample-size -1) distribution at <math>{\alpha\over 2}</math>]]. | ||
| + | |||
| + | Both the confidence intervals and the hypothesis testing methods in the paired design require Normality of both samples. If these parametric assumptions are invalid we must use a [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair | not-parametric (distribution free test)]], even if the latter is less powerful. | ||
| + | |||
| + | ===[[EBook#Chapter_VIII:_Hypothesis_Testing | Hypothesis Testing]] about the Difference of Means=== | ||
| + | * Null Hypothesis: <math>H_o: \mu_1-\mu_2=\mu_o</math> (e.g., <math>\mu_1-\mu_2=0</math>) | ||
| + | * Alternative Research Hypotheses: | ||
| + | ** One sided (uni-directional): <math>H_1: \mu_1 -\mu_2>\mu_o</math>, or <math>H_1: \mu_1-\mu_2<\mu_o</math> | ||
| + | ** Double sided: <math>H_1: \mu_1 - \mu_2 \not= \mu_o</math> | ||
| + | |||
| + | ====Test Statistics==== | ||
| + | * If the two populations that the {<math>X_i</math>} and {<math>Y_i</math>} samples were drawn from are approximately Normal, then the [http://en.wikipedia.org/wiki/Hypothesis_testing#Common_test_statistics Test Statistics] is: | ||
| + | : <math>T_o = {\overline{d} - \mu_o \over SE(\overline{d})} = {\overline{d} - \mu_o \over {{1\over \sqrt{n}} \sqrt{\sum_{i=1}^n{(d_i-\overline{d})^2\over n-1}}}} \sim T_{(df=n-1)}</math>. | ||
| + | |||
| + | ====Effects of Ignoring the Pairing==== | ||
| + | The SE estimate will be '''smaller''' for correctly paired data. If we look within each sample at the data, we notice variation from one subject to the next. This information gets incorporated into the SE for the independent t-test via <math>s_1</math> and <math>s_2</math>. The original reason we paired was to try to control for some of this inter-subject variation, which is not of interest in the paired design. Notice that the inter-subject variation has no influence on the SE for the paired test, because only the differences were used in the calculation. The price of pairing is smaller degrees of freedom of the T-test. However, this can be compensated with a smaller SE if we had paired correctly. | ||
| + | |||
| + | '''Pairing''' is used to ''reduce'' bias and ''increase'' precision in our inference. By '''matching/blocking''' we can control variation due to extraneous variables. | ||
| + | |||
| + | For example, if two groups are matched on age, then a comparison between the groups is free of any bias due to a difference in age distribution. | ||
| + | |||
| + | Pairing is a strategy of design, not an analysis tool. Pairing needs to be carried out before the data are observed. It is not correct to use the observations to make pairs after the data has been collected. | ||
| + | |||
| + | ===Example=== | ||
| + | Suppose we measure the thickness of plaque (mm) in the carotid artery of 10 randomly selected patients with [http://www.heartcheckamerica.com/cas_more.htm mild atherosclerotic disease]. Two measurements are taken, thickness before treatment with Vitamin E (baseline) and after two years of taking Vitamin E daily. Formulate testable hypothesis and make inference about the effect of the treatment at <math>\alpha=0.05</math>. | ||
| + | |||
| + | *What makes this paired data rather than independent data? | ||
| + | |||
| + | * Why would we want to use pairing in this example? | ||
| + | |||
| + | ====Data in row format==== | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:55%" border="1" | ||
| + | |- | ||
| + | | Before || 0.66,0.72,0.85,0.62,0.59,0.63,0.64,0.7,0.73,0.68 | ||
| + | |- | ||
| + | | After || 0.6,0.65,0.79,0.63,0.54,0.55,0.62,0.67,0.68,0.64 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | ====Data in column format==== | ||
| + | <center> | ||
| + | {| class="wikitable" style="text-align:center; width:55%" border="1" | ||
| + | |- | ||
| + | ! Subject || Before || After || Difference | ||
| + | |- | ||
| + | | 1 || 0.66 || 0.60 || 0.06 | ||
| + | |- | ||
| + | | 2 || 0.72 || 0.65 || 0.07 | ||
| + | |- | ||
| + | | 3 || 0.85 || 0.79 || 0.06 | ||
| + | |- | ||
| + | | 4 || 0.62 || 0.63 || -0.01 | ||
| + | |- | ||
| + | | 5 || 0.59 || 0.54 || 0.05 | ||
| + | |- | ||
| + | | 6 || 0.63 || 0.55 || 0.08 | ||
| + | |- | ||
| + | | 7 || 0.64 || 0.62 || 0.02 | ||
| + | |- | ||
| + | | 8 || 0.70 || 0.67 || 0.03 | ||
| + | |- | ||
| + | | 9 || 0.73 || 0.68 || 0.05 | ||
| + | |- | ||
| + | | 10 || 0.68 || 0.64 || 0.04 | ||
| + | |- | ||
| + | ! Mean || 0.682 || 0.637 || 0.045 | ||
| + | |- | ||
| + | ! SD || 0.0742 || 0.0709 || 0.0264 | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | ====[[AP_Statistics_Curriculum_2007_EDA_Plots |Exploratory Data Analysis]]==== | ||
| + | We begin first by exploring the data visually using various [[AP_Statistics_Curriculum_2007_EDA_Plots | SOCR EDA Tools]]. | ||
| + | |||
| + | * [[SOCR_EduMaterials_Activities_LineChart | Line Chart]] of the two samples | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig1.jpg|600px]]</center> | ||
| + | |||
| + | * [[SOCR_EduMaterials_Activities_BoxPlot| Box-And-Whisker Plot]] of the two samples | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig2.jpg|600px]]</center> | ||
| + | |||
| + | * [[SOCR_EduMaterials_Activities_IndexChart | Index plot]] of the differences | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig3.jpg|600px]]</center> | ||
| + | |||
| + | ====Inference==== | ||
| + | * Null Hypothesis: <math>H_o: \mu_{before}-\mu_{after}=0</math> | ||
| + | * (One-sided) Alternative Research Hypotheses: <math>H_1: \mu_{before} -\mu_{after}>0</math>. | ||
| + | |||
| + | * Test statistics: We can use the sample summary statistics to compute the [[AP_Statistics_Curriculum_2007_Infer_2Means_Dep#Test_Statistics |T-statistic]]: <math>T_o = {\overline{d} - \mu_o \over SE(\overline{d})} \sim T(df=9)</math> | ||
| + | : <math>T_o = {\overline{d} - \mu_o \over SE(\overline{d})} = {0.045 - 0 \over {{1\over \sqrt{10}} \sqrt{\sum_{i=1}^{10}{(d_i-0.045)^2\over 9}}})}= {0.045 \over 0.00833}=5.4022</math>. | ||
| + | |||
| + | : <math>p-value=P(T_{(df=9)}>T_o=5.4022)=0.000216</math> for this (one-sided) test. | ||
| + | |||
| + | Therefore, we '''can reject''' the null hypothesis at <math>\alpha=0.05</math>! The left white area at the tails of the T(df=9) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.000216, which is much smaller than the initially set [[AP_Statistics_Curriculum_2007_Hypothesis_Basics | Type I]] error <math>\alpha = 0.05</math> and we reject the null hypothesis. | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig4.jpg|600px]]</center> | ||
| + | |||
| + | * You can also use the [http://socr.ucla.edu/htmls/SOCR_Analyses.html SOCR Analyses (One-Sample T-Test)] to carry out these calculations as shown in the figure below. | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig5.jpg|600px]]</center> | ||
| + | |||
| + | * This [[SOCR_EduMaterials_AnalysisActivities_OneT | SOCR One Sample T-test Activity]] provides additional hands-on demonstrations of the one-sample hypothesis testing for the difference in paired experiments. | ||
| + | |||
| + | * <math>95%=(1-0.05)100%</math> (<math>\alpha=0.05</math>) Confidence interval (before-after): | ||
| + | : <math>CI(\mu_{before}-\mu_{after})</math>: <math>\overline{d} \pm t_{\alpha\over 2} SE(\overline {d}) = 0.045 \pm 1.833 \times 0.00833 = [0.0297 ; 0.0603].</math> | ||
| + | |||
| + | ====Conclusion==== | ||
| + | These data show that the true mean thickness of plaque after two years of treatment with Vitamin E is statistically significantly different than before the treatment (p =0.000216). In other words, vitamin E appears to be an effective in changing carotid artery plaque after treatment. The practical effect does appear to be < 60 microns; however, this may be clinically sufficient and justify patient treatment. | ||
| + | |||
| + | ====Paired Test Validity==== | ||
| + | Both the confidence intervals and the hypothesis testing methods in the paired design require Normality of both samples. If these parametric assumptions are invalid, we must use a [[AP_Statistics_Curriculum_2007_NonParam_2MedianPair | not-parametric (distribution free test)]], even if the latter is less powerful. | ||
| + | |||
| + | The plots below indicate that Normal assumptions are not unreasonable for these data, and hence we may be justified in using the one-sample T-test in this case. | ||
| + | |||
| + | * [[AP_Statistics_Curriculum_2007_Normal_Prob#Assessing_Normality |Quantile-Quantile Data-Data plot]] of the two datasets: | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig6.jpg|600px]]</center> | ||
| + | |||
| + | * [[AP_Statistics_Curriculum_2007_Normal_Prob#Assessing_Normality | QQ-Normal plot]] of the before data: | ||
| + | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Dep_020908_Fig7.jpg|600px]]</center> | ||
| + | |||
| + | ====Paired vs. Independent Testing==== | ||
| + | Suppose we accidentally analyzed the groups independently (using the [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |independent T-test]]) rather than using this paired test (this would be an incorrect way of analyzing this ''before-after'' data). How would this change our results and findings? | ||
| + | : \(T_o = {\overline{x}-\overline{y} - \mu_o \over SE(\overline{x}+\overline{y})} \sim T(df=17)\) | ||
| + | : \(T_o = {\overline{x}-\overline{y} - \mu_o \over SE(\overline{x}+\overline{y})} = {0.682 -0.637- 0 \over \sqrt{SE^2(\overline{x})+SE^2(\overline{y})}}= \) \({0.682 -0.637\over \sqrt{{0.0742^2\over 10}+ {0.0709^2\over 10}}}={0.682 -0.637\over 0.0325}=1.38\) | ||
| + | : \(p-value=P(T>1.38)= 0.100449\) and we would have failed to reject the null-hypothesis ('''[[AP_Statistics_Curriculum_2007_Infer_2Means_Dep#Inference|incorrect!]]''') | ||
| + | |||
| + | Similarly, had we incorrectly used the [[AP_Statistics_Curriculum_2007_Infer_2Means_Indep |independent design]] and constructed a corresponding Confidence interval, we would obtain an incorrect inference: | ||
| + | : \(CI: {\overline{x}-\overline{y} - \mu_o \pm t_{(df=17, \alpha/2)} \times SE(\overline{x}+\overline{y})} = \) \(0.045 \pm 1.740\times 0.0325 = [-0.0116 ; 0.1016].\) | ||
<hr> | <hr> | ||
| - | === | + | |
| - | + | ===[[EBook_Problems_Infer_2Means_Dep|Problems]]=== | |
<hr> | <hr> | ||
Current revision as of 19:59, 17 June 2013
Contents
|
General Advance-Placement (AP) Statistics Curriculum - Inferences about Two Means: Dependent Samples
In the previous chapter we saw how to do significance testing in the case of a single random sample. Now, we show how to do hypothesis testing comparing two samples and we begin with the simple case of paired samples.
Inferences About Two Means: Dependent Samples
In all study designs, it is always critical to clearly identify whether samples we compare come from dependent or independent populations. There is a general formulation for the significance testing when the samples are independent. The fact that there may be uncountable many different types of dependencies that prevents us from having a similar analysis protocol for all dependent sample cases. However, in one specific case - paired samples - we have a theory to generalize the significance testing analysis protocol. Two populations (or samples) are dependent because of pairing (or paired) if they are linked in some way, usually by a direct relationship. For example, measure the weight of subjects before and after a six month diet.
Paired Designs
These are the most common Paired Designs, in which the idea of pairing is that members of a pair are similar to each other with respect to extraneous variables.
- Randomized block experiments with two units per block
- Observational studies with individually matched controls (e.g., clinical trials of drug efficacy - patient pre vs. post treatment results are compared)
- Repeated (time or treatment affected) measurements on the same individual
- Blocking by time – formed implicitly when replicate measurements are made at different times.
Background
- Recall that for a random sample {
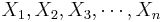 } of the process, the population mean may be estimated by the sample average,
} of the process, the population mean may be estimated by the sample average, 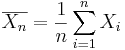 .
.
- The standard error of
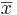 is given by
is given by 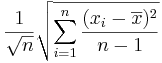 .
.
Analysis Protocol for Paired Designs
To study paired data, we would like to examine the differences between each pair. Suppose {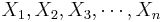 } and {
} and {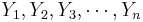 } represent the 2 paired samples. Then we want to study the difference sample {
} represent the 2 paired samples. Then we want to study the difference sample {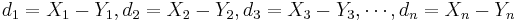 }. Notice the effect of the pairings of each Xi and Yi.
}. Notice the effect of the pairings of each Xi and Yi.
Now we can clearly see that the group effect (group differences) is directly represented in the {di} sequence. The one-sample T test is the proper strategy to analyze the difference sample {di}, if the Xi and Yi samples come from Normal distributions.
Since we are focusing on the differences, we can use the same reasoning as we did in the single sample case to calculate the standard error (i.e., the standard deviation of the sampling distribution of 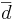 ) of
) of 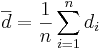 .
.
Thus, the standard error of 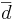 is given by
is given by 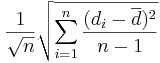 , where
, where 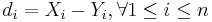 .
.
Confidence Interval of the Difference of Means
The interval estimation of the difference of two means (or Confidence intervals) is constructed as follows. Choose a confidence level (1 − α)100%, where α is small (e.g., 0.1, 0.05, 0.025, 0.01, 0.001, etc.). Then a (1 − α)100% confidence interval for μ1 − μ2 is defined in terms of the T-distribution:
Both the confidence intervals and the hypothesis testing methods in the paired design require Normality of both samples. If these parametric assumptions are invalid we must use a not-parametric (distribution free test), even if the latter is less powerful.
Hypothesis Testing about the Difference of Means
- Null Hypothesis: Ho:μ1 − μ2 = μo (e.g., μ1 − μ2 = 0)
- Alternative Research Hypotheses:
- One sided (uni-directional): H1:μ1 − μ2 > μo, or H1:μ1 − μ2 < μo
- Double sided:
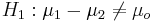
Test Statistics
- If the two populations that the {Xi} and {Yi} samples were drawn from are approximately Normal, then the Test Statistics is:
-
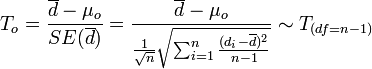 .
.
Effects of Ignoring the Pairing
The SE estimate will be smaller for correctly paired data. If we look within each sample at the data, we notice variation from one subject to the next. This information gets incorporated into the SE for the independent t-test via s1 and s2. The original reason we paired was to try to control for some of this inter-subject variation, which is not of interest in the paired design. Notice that the inter-subject variation has no influence on the SE for the paired test, because only the differences were used in the calculation. The price of pairing is smaller degrees of freedom of the T-test. However, this can be compensated with a smaller SE if we had paired correctly.
Pairing is used to reduce bias and increase precision in our inference. By matching/blocking we can control variation due to extraneous variables.
For example, if two groups are matched on age, then a comparison between the groups is free of any bias due to a difference in age distribution.
Pairing is a strategy of design, not an analysis tool. Pairing needs to be carried out before the data are observed. It is not correct to use the observations to make pairs after the data has been collected.
Example
Suppose we measure the thickness of plaque (mm) in the carotid artery of 10 randomly selected patients with mild atherosclerotic disease. Two measurements are taken, thickness before treatment with Vitamin E (baseline) and after two years of taking Vitamin E daily. Formulate testable hypothesis and make inference about the effect of the treatment at α = 0.05.
- What makes this paired data rather than independent data?
- Why would we want to use pairing in this example?
Data in row format
| Before | 0.66,0.72,0.85,0.62,0.59,0.63,0.64,0.7,0.73,0.68 |
| After | 0.6,0.65,0.79,0.63,0.54,0.55,0.62,0.67,0.68,0.64 |
Data in column format
| Subject | Before | After | Difference |
|---|---|---|---|
| 1 | 0.66 | 0.60 | 0.06 |
| 2 | 0.72 | 0.65 | 0.07 |
| 3 | 0.85 | 0.79 | 0.06 |
| 4 | 0.62 | 0.63 | -0.01 |
| 5 | 0.59 | 0.54 | 0.05 |
| 6 | 0.63 | 0.55 | 0.08 |
| 7 | 0.64 | 0.62 | 0.02 |
| 8 | 0.70 | 0.67 | 0.03 |
| 9 | 0.73 | 0.68 | 0.05 |
| 10 | 0.68 | 0.64 | 0.04 |
| Mean | 0.682 | 0.637 | 0.045 |
| SD | 0.0742 | 0.0709 | 0.0264 |
Exploratory Data Analysis
We begin first by exploring the data visually using various SOCR EDA Tools.
- Line Chart of the two samples
- Box-And-Whisker Plot of the two samples
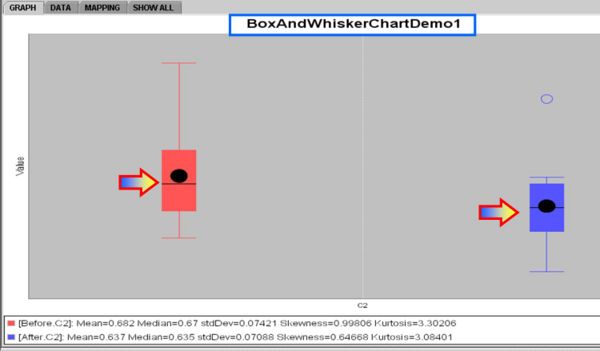
- Index plot of the differences
Inference
- Null Hypothesis: Ho:μbefore − μafter = 0
- (One-sided) Alternative Research Hypotheses: H1:μbefore − μafter > 0.
- Test statistics: We can use the sample summary statistics to compute the T-statistic:
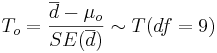
-
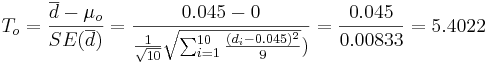 .
.
- p − value = P(T(df = 9) > To = 5.4022) = 0.000216 for this (one-sided) test.
Therefore, we can reject the null hypothesis at α = 0.05! The left white area at the tails of the T(df=9) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.000216, which is much smaller than the initially set Type I error α = 0.05 and we reject the null hypothesis.
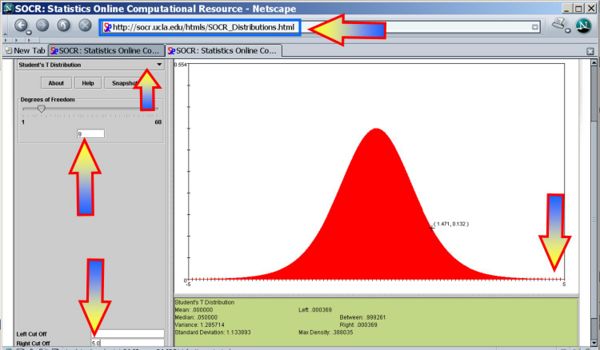
- You can also use the SOCR Analyses (One-Sample T-Test) to carry out these calculations as shown in the figure below.
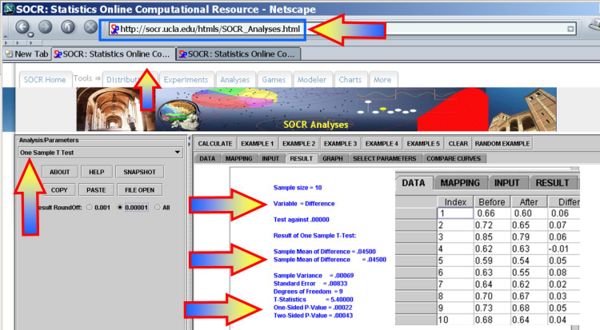
- This SOCR One Sample T-test Activity provides additional hands-on demonstrations of the one-sample hypothesis testing for the difference in paired experiments.
- 95% = (1 − 0.05)100% (α = 0.05) Confidence interval (before-after):
- CI(μbefore − μafter):
![\overline{d} \pm t_{\alpha\over 2} SE(\overline {d}) = 0.045 \pm 1.833 \times 0.00833 = [0.0297 ; 0.0603].](/socr/uploads/math/2/5/6/25608769a5219a56b2273efc7c03f0c9.png)
Conclusion
These data show that the true mean thickness of plaque after two years of treatment with Vitamin E is statistically significantly different than before the treatment (p =0.000216). In other words, vitamin E appears to be an effective in changing carotid artery plaque after treatment. The practical effect does appear to be < 60 microns; however, this may be clinically sufficient and justify patient treatment.
Paired Test Validity
Both the confidence intervals and the hypothesis testing methods in the paired design require Normality of both samples. If these parametric assumptions are invalid, we must use a not-parametric (distribution free test), even if the latter is less powerful.
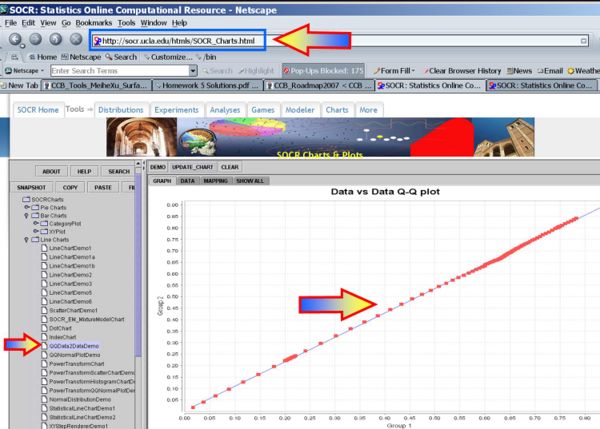
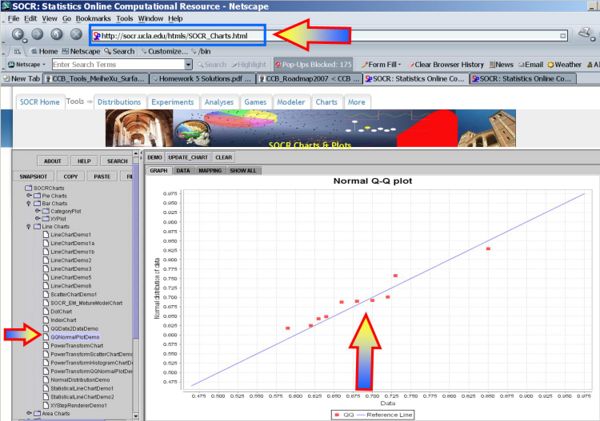
The plots below indicate that Normal assumptions are not unreasonable for these data, and hence we may be justified in using the one-sample T-test in this case.
- Quantile-Quantile Data-Data plot of the two datasets:
- QQ-Normal plot of the before data:
Paired vs. Independent Testing
Suppose we accidentally analyzed the groups independently (using the independent T-test) rather than using this paired test (this would be an incorrect way of analyzing this before-after data). How would this change our results and findings?
- \(T_o = {\overline{x}-\overline{y} - \mu_o \over SE(\overline{x}+\overline{y})} \sim T(df=17)\)
- \(T_o = {\overline{x}-\overline{y} - \mu_o \over SE(\overline{x}+\overline{y})} = {0.682 -0.637- 0 \over \sqrt{SE^2(\overline{x})+SE^2(\overline{y})}}= \) \({0.682 -0.637\over \sqrt{{0.0742^2\over 10}+ {0.0709^2\over 10}}}={0.682 -0.637\over 0.0325}=1.38\)
- \(p-value=P(T>1.38)= 0.100449\) and we would have failed to reject the null-hypothesis (incorrect!)
Similarly, had we incorrectly used the independent design and constructed a corresponding Confidence interval, we would obtain an incorrect inference:
- \(CI: {\overline{x}-\overline{y} - \mu_o \pm t_{(df=17, \alpha/2)} \times SE(\overline{x}+\overline{y})} = \) \(0.045 \pm 1.740\times 0.0325 = [-0.0116 ; 0.1016].\)
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
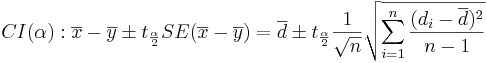
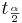 is the
is the