AP Statistics Curriculum 2007 Infer 2Means Indep
From Socr
m (→Inference: typo) |
|||
| Line 33: | Line 33: | ||
===Example=== | ===Example=== | ||
| - | Nine observations of surface soil [http://en.wikipedia.org/wiki/PH pH] were made at two different locations. Does the data suggest that the true mean soil [http://en.wikipedia.org/wiki/PH pH] values | + | Nine observations of surface soil [http://en.wikipedia.org/wiki/PH pH] were made at two different locations. Does the data suggest that the true mean soil [http://en.wikipedia.org/wiki/PH pH] values differs for the two locations? Formulate testable hypothesis and make inference about the effect of the treatment at <math>\alpha=0.05</math>. Check any necessary assumptions for the validity of your test. |
====Data in row format==== | ====Data in row format==== | ||
| Line 95: | Line 95: | ||
: <math>t_o = {7.9322-7.460-0 \over 0.081}=5.829</math>. | : <math>t_o = {7.9322-7.460-0 \over 0.081}=5.829</math>. | ||
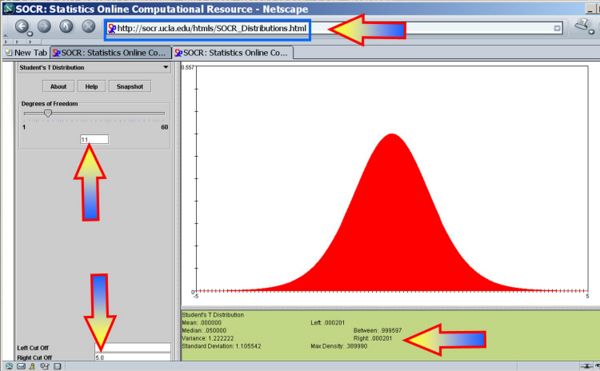
| - | : <math>p-value=P(T_{(df=11)}>T_o=5.829)=0.00003</math> for this (two-sided) test. Therefore, we '''can reject''' the null hypothesis at <math>\alpha=0.05</math>! The left white area at the tails of the T(df=11) distribution | + | : <math>p-value=P(T_{(df=11)}>T_o=5.829)=0.00003</math> for this (two-sided) test. Therefore, we '''can reject''' the null hypothesis at <math>\alpha=0.05</math>! The left white area at the tails of the T(df=11) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.00003, which is much smaller than the initially set [[AP_Statistics_Curriculum_2007_Hypothesis_Basics | Type I]] error <math>\alpha = 0.05</math> and we reject the null hypothesis. |
<center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Indep_020908_Fig4.jpg|600px]]</center> | <center>[[Image:SOCR_EBook_Dinov_Infer_2Means_Indep_020908_Fig4.jpg|600px]]</center> | ||
Revision as of 17:22, 28 June 2010
Contents |
General Advance-Placement (AP) Statistics Curriculum - Inferences about Two Means: Independent Samples
In the previous section we discussed the inference on two paired random samples. Now, we show how to do inference on two independent samples.
Indepenent Samples Designs
Independent samples designs refer to design of experiments or observations where all measurements are individually independent from each other within their groups and the groups are independent. The groups may be drawn from different populations with different distribution characteristics.
Background
- Recall that for a random sample {
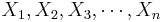 } of the process, the population mean may be estimated by the sample average,
} of the process, the population mean may be estimated by the sample average, 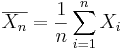 .
.
- The standard error of
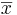 is given by
is given by 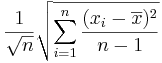 .
.
Analysis Protocol for Independent Designs
To study independent samples, we would like to examine the differences between two group means. Suppose {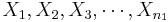 } and {
} and {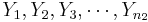 } represent the two independent samples. Then we want to study the differences of the two group means relative to the internal sample variations. If the two samples were drawn from populations that had different centers, then we would expect that the two sample averages will be distinct.
} represent the two independent samples. Then we want to study the differences of the two group means relative to the internal sample variations. If the two samples were drawn from populations that had different centers, then we would expect that the two sample averages will be distinct.
Large Samples
- Significance Testing: We have a standard null-hypothesis Ho:μX − μY = μo (e.g., μo = 0). Then the test statistics is:
-
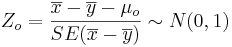 .
.
-
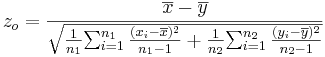
- Confidence Intervals: (1 − α)100% confidence interval for μ1 − μ2 will be
-
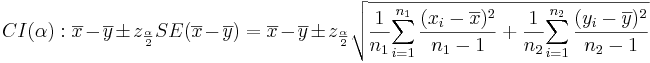 . Note that the
. Note that the 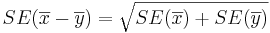 , as the samples are independent. Also,
, as the samples are independent. Also,  is the critical value for a Standard Normal distribution at
is the critical value for a Standard Normal distribution at 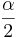 .
.
Small Samples
- Significance Testing: Again, we have a standard null-hypothesis Ho:μX − μY = μo (e.g., μo = 0). Then the test statistics is:
-
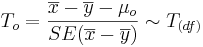 .
.
- The degrees of freedom (df) is:
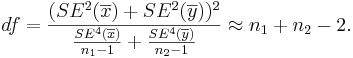 Always round down the degrees of freedom to the next smaller integer.
Always round down the degrees of freedom to the next smaller integer.
-
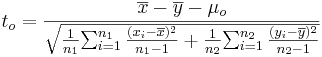
- Confidence Intervals: (1 − α)100% confidence interval for μ1 − μ2 will be
-
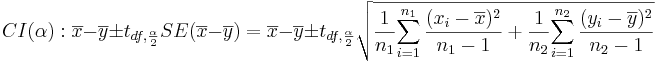 . Note that the
. Note that the 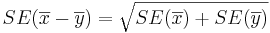 , as the samples are independent.
, as the samples are independent.
- The degrees of freedom is:
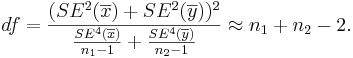 Always round down the degrees of freedom to the next smaller integer. Also,
Always round down the degrees of freedom to the next smaller integer. Also, 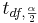 is the critical value for a Student's T distribution at
is the critical value for a Student's T distribution at 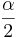 .
.
Example
Nine observations of surface soil pH were made at two different locations. Does the data suggest that the true mean soil pH values differs for the two locations? Formulate testable hypothesis and make inference about the effect of the treatment at α = 0.05. Check any necessary assumptions for the validity of your test.
Data in row format
| Location 1 | 8.1,7.89,8,7.85,8.01,7.82,7.99,7.8,7.93 |
| Location 2 | 7.85,7.3,7.73,7.27,7.58,7.27,7.5,7.23,7.41 |
Data in column format
| Index | Location 1 | Location 2 |
|---|---|---|
| 1 | 8.10 | 7.85 |
| 2 | 7.89 | 7.30 |
| 3 | 8.00 | 7.73 |
| 4 | 7.85 | 7.27 |
| 5 | 8.01 | 7.58 |
| 6 | 7.82 | 7.27 |
| 7 | 7.99 | 7.50 |
| 8 | 7.80 | 7.23 |
| 9 | 7.93 | 7.41 |
| Mean | 7.9322 | 7.4600 |
| SD | 0.1005 | 0.2220 |
Exploratory Data Analysis
We begin first by exploring the data visually using various SOCR EDA Tools.
- Line Chart of the two samples
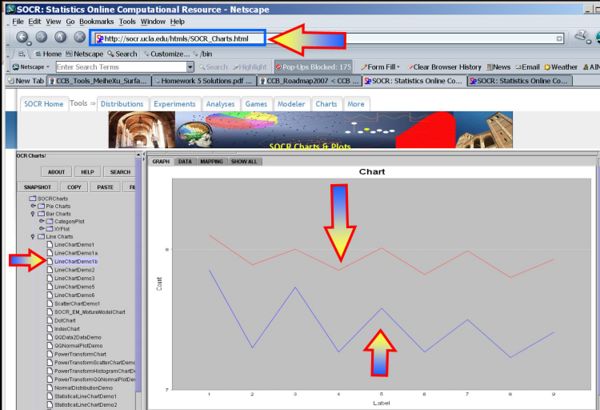
- Box-And-Whisker Plot of the two samples
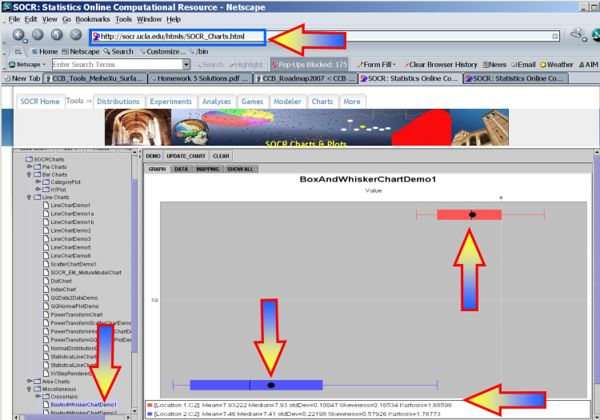
Inference
- Null Hypothesis: Ho:μ1 − μ2 = 0
- (Two-sided) alternative Research Hypotheses:
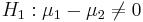 .
.
- Test statistics: We can use the sample summary statistics to compute the degrees of freedom and the T-statistic
- The degrees of freedom is:
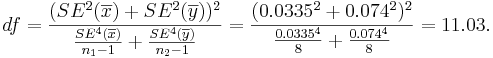 So, we round down df=11.
So, we round down df=11.
-
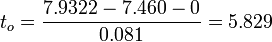 .
.
- p − value = P(T(df = 11) > To = 5.829) = 0.00003 for this (two-sided) test. Therefore, we can reject the null hypothesis at α = 0.05! The left white area at the tails of the T(df=11) distribution depicts graphically the probability of interest, which represents the strength of the evidence (in the data) against the Null hypothesis. In this case, this area is 0.00003, which is much smaller than the initially set Type I error α = 0.05 and we reject the null hypothesis.
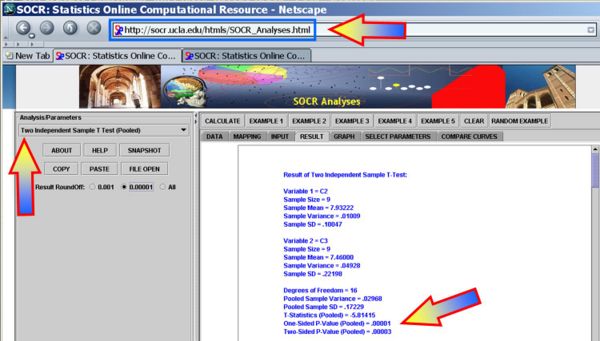
- You can also use the SOCR Analyses (Two-Independent Samples T-Test) to carry out these calculations as shown in the figure below.
- This SOCR Two-Sample Independent T-test Activity provides additional hands-on demonstrations of the two-sample hypothesis testing.
- 95% = (1 − 0.05)100% (α = 0.05) Confidence interval:
- CI(μ1 − μ2):
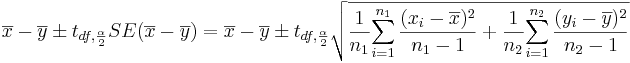
Conclusion
These data show that there is a statistically significant mean difference in the pH of Location 1 and Location 2 (p < 0.001).
Independent T-test Validity
Both the confidence intervals and the hypothesis testing methods in the independent-sample design require Normality of both samples. If the sample sizes are large (say >50), Normality is not as critical, as the CLT implies the sampling distributions of the means are approximately Normal. If these parametric assumptions are invalid we must use a non-parametric (distribution free test), even if the latter is less powerful.
The plots below indicate that Normal assumptions are not unreasonable for these data, and hence we may be justified in using the two independent sample T-test in this case.
- QQ-Normal plot of the first sample:
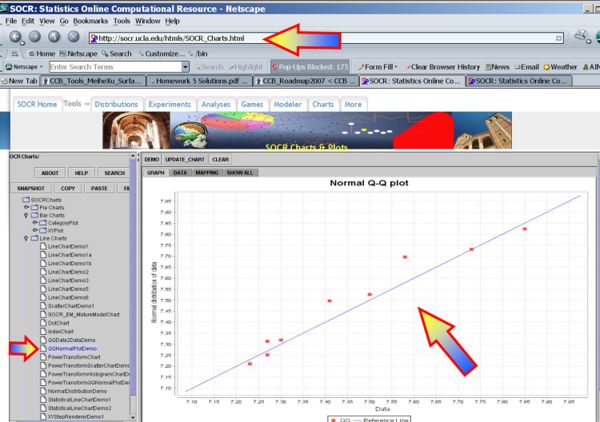
- QQ-Normal plot of the second sample:
Problems
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
![CI: {7.932-7.460 \pm 2.201\times 0.081 }= [0.294 ; 0.650].](/socr/uploads/math/2/8/6/286be017d1a16fb1a788ec44a8c2b566.png)
