AP Statistics Curriculum 2007 Infer 2Proportions
From Socr
(→Testing for equality of Two Proportions) |
(→Testing for equality of Two Proportions) |
||
| Line 8: | Line 8: | ||
1,& \texttt{Characteristic-present}.\end{cases}</math> | 1,& \texttt{Characteristic-present}.\end{cases}</math> | ||
| - | Since the raw sample proportions of observations having the characteristic of interest are | + | Since the ''raw sample proportions'' of observations having the characteristic of interest are |
: <math>\hat{p_x}={1 \over n}\sum_{i=1}^n{x_i}</math> and <math>\hat{p_y}={1 \over k}\sum_{i=1}^k{y_i}</math> | : <math>\hat{p_x}={1 \over n}\sum_{i=1}^n{x_i}</math> and <math>\hat{p_y}={1 \over k}\sum_{i=1}^k{y_i}</math> | ||
| - | The corrected sample proportions (for small samples) are | + | The ''corrected sample proportions'' (for small samples) are |
| - | : <math>\tilde{p_x}={\sum_{i=1}^n{x_i}+0.5z_{\alpha \over 2}^2 \over n+z_{\alpha \over 2}^2},</math> | + | : <math>\tilde{p_x}={\sum_{i=1}^n{x_i}+0.5z_{\alpha \over 2}^2 \over n+z_{\alpha \over 2}^2},</math> and <math>\tilde{p_y}={\sum_{i=1}^k{y_i}+0.5z_{\alpha \over 2}^2 \over k+z_{\alpha \over 2}^2},</math> |
| - | + | ||
where [[AP_Statistics_Curriculum_2007_Normal_Critical | <math>z_{\alpha \over 2}</math> is the normal critical value we saw earlier]]. | where [[AP_Statistics_Curriculum_2007_Normal_Critical | <math>z_{\alpha \over 2}</math> is the normal critical value we saw earlier]]. | ||
By the independence of the samples, the standard error of the difference of the two proportion estimates is: | By the independence of the samples, the standard error of the difference of the two proportion estimates is: | ||
| - | : <math>SE_{\hat{p_x}-\hat{p_y}} = \sqrt{SE_{\hat{p_x}}^2 + SE_{\hat{p_y}}^2}= \sqrt{ {\hat{p_x}(1-\hat{p_x})\over n} + {\hat{p_y}(1-\hat{p_y})\over k}}.</math> | + | : '''Raw proportions''': <math>SE_{\hat{p_x}-\hat{p_y}} = \sqrt{SE_{\hat{p_x}}^2 + SE_{\hat{p_y}}^2}= \sqrt{ {\hat{p_x}(1-\hat{p_x})\over n} + {\hat{p_y}(1-\hat{p_y})\over k}}.</math> |
| - | : <math>SE_{\tilde{p_x}-\tilde{p_y}} = \sqrt{SE_{\tilde{p_x}}^2 + SE_{\tilde{p_y}}^2}= \sqrt{ {\tilde{p_x}(1-\tilde{p_x})\over n+z_{\alpha \over 2}^2} + {\tilde{p_y}(1-\tilde{p_y})\over k+z_{\alpha \over 2}^2}}.</math> | + | : '''Corrected Proportions''': <math>SE_{\tilde{p_x}-\tilde{p_y}} = \sqrt{SE_{\tilde{p_x}}^2 + SE_{\tilde{p_y}}^2}= \sqrt{ {\tilde{p_x}(1-\tilde{p_x})\over n+z_{\alpha \over 2}^2} + {\tilde{p_y}(1-\tilde{p_y})\over k+z_{\alpha \over 2}^2}}.</math> |
=== Hypothesis Testing the difference of Two Proportions=== | === Hypothesis Testing the difference of Two Proportions=== | ||
Revision as of 00:27, 17 February 2008
Contents |
General Advance-Placement (AP) Statistics Curriculum - Inferences about Two Proportions
Testing for equality of Two Proportions
Suppose we have two populations and we are interested in estimating whether the proportions of subjects that have certain characteristic of interest (e.g., fixed gender) in each population are equal. To make this inference we obtain two samples {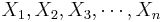 } and {
} and {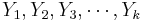 }, where each Xi and Yi represents whether the ith observation in the sample had the characteristic of interest. That is
}, where each Xi and Yi represents whether the ith observation in the sample had the characteristic of interest. That is
-
 and
and 
Since the raw sample proportions of observations having the characteristic of interest are
-
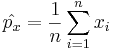 and
and 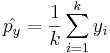
The corrected sample proportions (for small samples) are
-
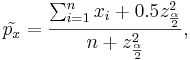 and
and 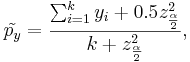
where  is the normal critical value we saw earlier.
is the normal critical value we saw earlier.
By the independence of the samples, the standard error of the difference of the two proportion estimates is:
- Raw proportions:
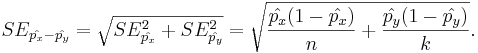
- Corrected Proportions:
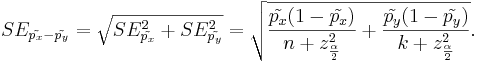
Hypothesis Testing the difference of Two Proportions
- Null Hypothesis: Ho:px = py, where px and px are the sample population proportions of interest.
- Alternative Research Hypotheses:
- One sided (uni-directional): H1:px > py, or Ho:px < py
- Double sided:
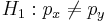
- Test Statistics:
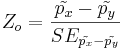
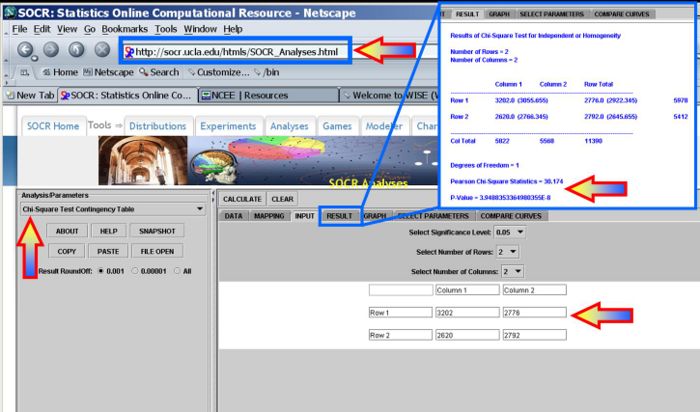
Genders of Siblings Example
Is the gender of a second child influenced by the gender of the first child, in families with >1 kid? Research hypothesis needs to be formulated first before collecting/looking/interpreting the data that will be used to address it. Mothers whose 1st child is a girl are more likely to have a girl, as a second child, compared to mothers with boys as 1st children. Data: 20 yrs of birth records of 1 Hospital in Auckland, New Zealand.
| Second Child | ||||
| Male | Female | Total | ||
| First Child | Male | 3,202 | 2,776 | 5,978 |
| Female | 2,620 | 2,792 | 5,412 | |
| Total | 5,822 | 5,568 | 11,390 | |
Let p1=true proportion of girls in mothers with girl as first child, p2=true proportion of girls in mothers with boy as first child. The parameter of interest is p1 − p2.
- Hypotheses: Ho:p1 − p2 = 0 (skeptical reaction). H1:p1 − p2 > 0 (research hypothesis).
| Second Child | ||||
| Number of births | Number of girls | Proportion | ||
| Group | 1 (Previous child was girl) | n1 = 5412 | 2792 | 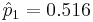
|
| 2 (Previous child was boy) | n2 = 5978 | 2776 | 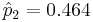
| |
- Test Statistics:
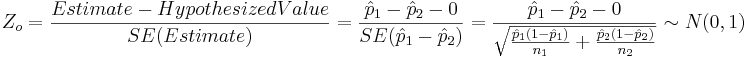 and Zo = 5.4996.
and Zo = 5.4996.
-
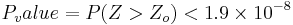 . This small p-values provides extremely strong evidence to reject the null hypothesis that there are no differences between the proportions of mothers that had a girl as a second child but had either boy or girl as their first child. Hence there is strong statistical evidence implying that genders of siblings are not independent.
. This small p-values provides extremely strong evidence to reject the null hypothesis that there are no differences between the proportions of mothers that had a girl as a second child but had either boy or girl as their first child. Hence there is strong statistical evidence implying that genders of siblings are not independent.
- Practical significance: The practical significance of the effect (of the gender of the first child on the gender of the second child, in this case) can only be assessed using confidence intervals. A 95% CI(p1 − p2) = [0.033;0.070] is computed by
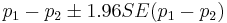 . Clearly, this is a practically negligible effect and no reasonable person would make important prospective family decisions based on the gender of their (first) child.
. Clearly, this is a practically negligible effect and no reasonable person would make important prospective family decisions based on the gender of their (first) child.
- This SOCR Analysis Activity illustrates how to use the SOCR Analyses to compute the p-values and answer the hypothesis testing challenge.
References
- SOCR Home page: http://www.socr.ucla.edu
Translate this page:
